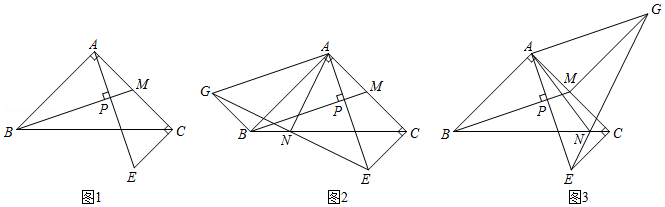
如图,在 中, , , 是 边上的一点,连接 ,作 于点 ,过点 作 的垂线交 的延长线于点 .
(1)如图1,求证: ;
(2)如图2,以 , 为邻边作平行四边形 ,连接 交 于点 ,连接 ,求 的值;
(3)如图3,若 是 的中点,以 , 为邻边作平行四边形 ,连接 交 于点 ,连接 ,经探究发现 ,请直接写出 的值.
如图,点O是边长为8的正方形ABCD边AD上一个动点(4<OA<8),以O为圆心、OA长为半径的圆交边CD于点M,连接OM,以CM为边在正方形ABCD内部作∠CMN=∠DOM,直线MN交边BC于点N.
(1)试说明:直线MN是⊙O的切线;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你有什么发现?
某饰品店老板去批发市场购买新款手链,第一次购手链共用100元,回来后该手链按定价2.8元销售,并很快售完.由于该手链深得“潮女”喜爱十分畅销,第二次去购手链时,每条的批发价已比第一次高0.5元,共用去了150元,所购数量比第一次多10条.当这批手链售出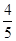 时,出现滞销,便以定价的5折售完剩余手链.(手链销售中不考虑其它因素)
时,出现滞销,便以定价的5折售完剩余手链.(手链销售中不考虑其它因素)
(1)求第一次该手链的批发价;
(2)试问该老板第二次销售手链是赔钱了,还是赚钱了?用数据说明.
如图,已知△ABC中,∠ABC=135°,过B作AB的垂线交AC于点P,若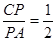 ,PB=2,求BC的长.
,PB=2,求BC的长.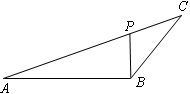
九(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 (t) (t) |
频数(户) |
频率 |
 |
6 |
0.12 |
 |
0.24 |
|
 |
16 |
0.32 |
 |
10 |
0.20 |
 |
4 |
|
 |
2 |
0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过20t的家庭大约有多少户?
一个不透明的布袋里装有红、黄、绿三种颜色的球(除颜色不同,其它均无任何区别),其中红球2个,黄球1个,从袋中任意摸出一个球是红球的概率是 .
.
(1)求布袋中绿球的个数;
(2)第一次从袋中任意摸出一个球,记下颜色后放回袋中,第二次再摸出一个球记下颜色,请用画树状图或列表的方法求两次都摸到红球的概率.