如图,  是
是  的直径,
,
的直径,
,  ,连接
,连接  .
.
(1)求证:  ;
;
(2)若直线  为
为  的切线,
的切线,  是切点,在直线
是切点,在直线  上取一点
上取一点  ,使
,使  ,
,  所在的直线与
所在的直线与  所在的直线相交于点
所在的直线相交于点  ,连接
,连接  .
.
①试探究  与
与  之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 是否为定值?若是,请求出这个定值;若不是,请说明理由.

如图,在直角坐标系中,⊙P与y轴相切于点C,与x轴交于A(x1,0),B(x2,0)两点,其中x1,x2是方程x2-10x+16=0的两个根,且x1<x2,连接BC,AC.
(1)求过A、B、C三点的抛物线的解析式;
(2)在抛物线的对称轴上是否存在点Q,使△QAC的周长最小,若存在求出点Q的坐标,若不存在,请说明理由;
(3)点M在第一象限的抛物线上,当△MBC的面积最大时,求点M的坐标.
4月20日8时2分,四川省雅安市芦山县发生了7.0级地震,当地的部分房屋严重受损,上万灾民无家可归,灾情牵动亿万中国人的心。某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资。已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
| 车 型 运往地 |
甲 地(元/辆) |
乙 地(元/辆) |
| 大货车 |
720 |
800 |
| 小货车 |
500 |
650 |
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为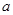 辆,前往甲、乙两地的总运费为w元,求出w与
辆,前往甲、乙两地的总运费为w元,求出w与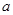 的函数关系式(写出自变量的取值范围);
的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费
如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(1)求证:AF=EF;
(2)求tan∠ABF的值;
(3)连接AC交BE于点G,求AG的长.
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长交AD于点E,交BA的延长线于点F.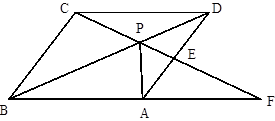
(1)求证:∠DCP=∠DAP;
(2)若AB=2,DP∶PB=1∶2,且PA⊥BF,求对角线BD的长.
如图,已知A(-4,n),B(1,-4)是一次函数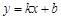 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.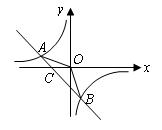
(1)求反比例函数和一次函数的解析式;
(2)求直线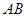 与
与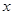 轴的交点
轴的交点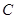 的坐标及△
的坐标及△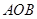 的面积;
的面积;
(3)求不等式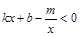 的解集(请直接写出答案).
的解集(请直接写出答案).