在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

先化简,再求值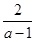 +
+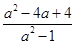 ·
·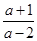 ,其中a=
,其中a= +1.
+1.
先化简,再求值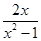 ÷
÷ -
- 其中x=2tan 45°.
其中x=2tan 45°.
先化简,再求值: ·
· ,其中a=-3.
,其中a=-3.
已知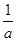 -
-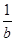 =
=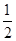 ,求
,求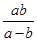 的值.
的值.
阅读下列材料,你能得到什么结论?并利用(1)的结论分解因式.
(1)形如x2+(p+q)x+pq型的二次三项式,有以下特点:①二次项系数是1;②常数项是两个数之积;③一次项系数是常数项的两个因数之和,把这个二次三项式进行分解因式,可以这样来解:
x2+(p+q)x+pq=x2+px+qx+pq
=(x2+px)+(qx+pq)=x(x+p)+q(x+p)
=(x+p)(x+q).
因此,可以得x2+(p+q)x+pq=________.
利用上面的结论,可以直接将某些二次项系数为1的二次三项式分解因式.
(2)利用(1)的结论分解因式:
①m2+7m-18;
②x2-2x-15.