已知 是等腰三角形,
是等腰三角形,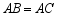 .
.
(1)特殊情形:如图1,当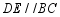 时,有
时,有
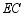 .(填“
.(填“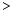 ”,“
”,“ 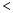 ”或“
”或“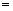 ”
” 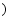
(2)发现探究:若将图1中的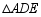 绕点
绕点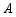 顺时针旋转
顺时针旋转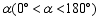 到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,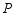 是等腰直角三角形
是等腰直角三角形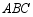 内一点,
内一点,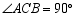 ,且
,且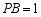 ,
,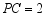 ,
,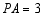 ,求
,求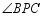 的度数.
的度数.
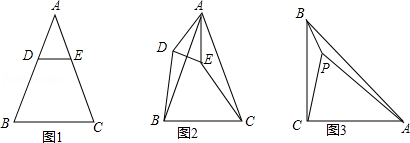
解不等式组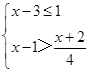 .
.
【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , = .
= .
(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
某水果超市以8元/千克的单价购进1000千克的苹果,为提高利润和便于销售,将苹果按大小分两种规格出售,计划大、小号苹果都为500千克,大号苹果单价定为16元/千克,小号苹果单价定为10元/千克,若大号苹果比计划每增加1千克,则大苹果单价减少0.03元,小号苹果比计划每减少1千克,则小苹果单价增加0.02元.设大号苹果比计划增加x千克.
(1)大号苹果的单价为 元/千克;小号苹果的单价为 元/千克;(用含x 的代数式表示)
(2)若水果超市售完购进的1000千克苹果,请解决以下问题:
①当x为何值时,所获利润最大?
②若所获利润为3385元,求x的值.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,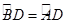 ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.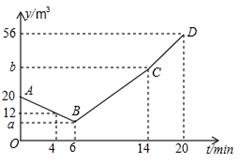

(1)每个出水口每分钟出水 m3,表格中a= ;
(2)求进水口每分钟的进水量和b的值;
(3)在整个过程中t为何值时,水池有水16m3