甲车从
地驶往
地，同时乙车从
地驶往
地，两车相向而行，匀速行驶，甲车距
地的距离
与行驶时间
之间的函数关系如图所示，乙车的速度是
（1）求甲车的速度；
（2）当甲乙两车相遇后，乙车速度变为
，并保持匀速行驶，甲车速度保持不变，结果乙车比甲车晚38分钟到达终点，求
的值．
）某商场服装部销售一种名牌衬衫，平均每天可售出30件，每件盈利40元．为了扩大销售，减少库存，商场决定降价销售，经调查，每件降价1元时，平均每天可多卖出2件．
（1）若商场要求该服装部每天盈利1200元，每件衬衫应降价多少元？
（2）试说明每件衬衫降价多少元时，商场服装部每天盈利最多．
设a，b，c是△ABC的三条边，关于x的方程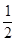
x2+
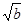x+c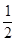－a=0有两个相等的实数根，方程3cx+2b=2a的根为x=0．
（1）试判断△ABC的形状．
（2）若a，b为方程x2+mx－3m=0的两个根，求m的值．
如图，是定远县统计局公布的2008～2011年全社会用电量的折线统计图．
（1）填写统计表：
2008～2011年定远县全社会用电量统计表:
| 年份 |
2008 |
2009 |
2010 |
2011 |
| 全社会用电量 （单位：亿kW·h） |
13.33 |
（2）根据定远县2009年至2011年全社会用电量统计数据，求这两年年平均增长的百分率（保留两个有效数字）．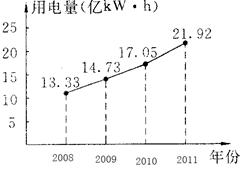
为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两间工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品？
如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
(1)求△ABC的面积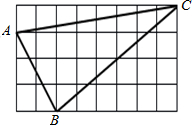
(2)判断△ABC是什么形状? 并说明理由.