如图，反比例函数
的图象与直线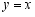
交于点
，
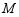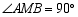，其两边分别与两坐标轴的正半轴交于点
，
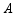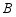，四边形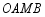
的面积为6．
（1）求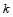
的值；
（2）点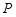
在反比例函数
的图象上，若点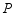
的横坐标为3，
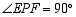，其两边分别与
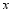轴的正半轴，直线
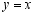交于点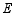
，
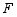，问是否存在点
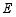，使得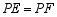
？若存在，求出点
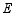的坐标；若不存在，请说明理由．
计算：
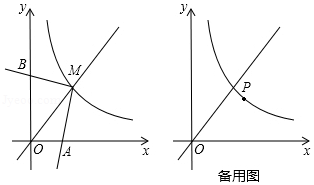
（1）（－2）2－（2－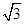
）0＋2·tan45°；
（2）先将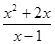
·（1－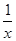
）化简，然后请自选一个你喜欢的x值，再求原式的值．
如图，在矩形ABCD中，AB=6cm，BC=8cm．如果点E由点B出发沿BC方
向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为2cm/s和1cm/s．FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t（s）（0＜t＜4）．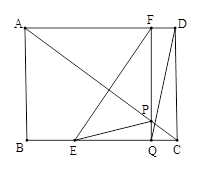
（1）连结EF、DQ，若四边形EQDF为平行四边形，求t的值；
（2）连结EP，设△EPC的面积为ycm2，求y与t的函数关系式，并求y的最大值；
（3）若△EPQ与△ADC相似，请直接写出t的值．
如图，AB为半圆O的直径，点C在半圆上，CD⊥AB于点D，连结BC，作∠BCP=∠BCD，CP交AB延长线于点P．
（1）求证：PC是半圆O的切线；
（2）求证：PC2=PB•PA；
（3）若PC=2，tan∠BCD=
，求
的长．
如图，抛物线
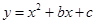与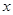
轴交于A（﹣2，0），B（6，0）两点．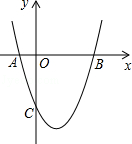
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）点P为y轴右侧抛物线上一个动点，若S△PAB=32，求出此时P点的坐标．
如图，正方形ABCD中，点F在AD上，点E在AB的延长线上，∠FCE=90°．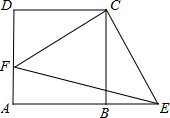
（1）求证：△CDF≌△CBE．
（2）若CD=8．EF=10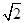
．求∠DCF的余弦值．