问题引入：如图，在△ABC中，D是BC上一点，AE=
AD，求
：
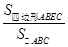尝试探究：过点A作BC的垂线，垂足为F，过点E作BC的垂线，垂足为G，如图所示，有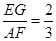
，
，
．
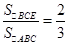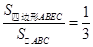类比延伸：若E为AD上的任一点，如图所示，试猜S四边形ABEC与S△ABC的比是图中哪条线段的比，并加以证明．
拓展应用：如图，E为△ABC内一点，射线AE于BC于点D，射线BE交AC于点F，射线CE交AB于点G，求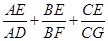
的值．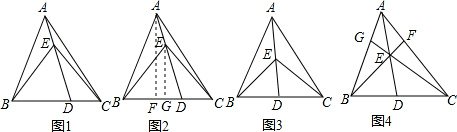
某课桌生产厂家研究发现，倾斜12°～24°的桌面有利于学生保持躯体
自然姿势．根据这一研究，厂家决定将水平桌面做成可调节角度的桌面．新桌面的设计
图如图1，AB可绕点A旋转，在点C处安装一根可旋转的支撑臂CD，AC＝30cm．
（1）如图2，当∠BAC＝24°时，CD⊥AB，求支撑臂CD的长；
（2）如图3，当∠BAC＝12°时，求AD的长．（结果保留根号）
（参考数据： sin24°≈0.40，cos24°≈0.91，tan24°≈0.46， sin12°≈0.20）
在一个不透明的盒子中，放入2个白球和1个红球，这些球除颜色外都相同．
（1）搅匀后从中任意摸出2个球，请通过列表或树状图求摸出2个球都是白球的概率；
（2）搅匀后从中任意摸出1个球，记录下颜色后放回袋中，再次搅匀后从中任意摸出1
个球，则2次摸出的球都是白色的概率为 ▲；
（3）现有一个可以自由转动的转盘，转盘被等分成60个相等的扇形，这些扇形除颜色
外完全相同，其中40个扇形涂上白色，20个扇形涂上红色，转动转盘2次，指针2次都
指向白色区域的
概率为 ▲．
如图，在四边形ABCD中，AD//BC，E、F为AB上两点，且△DAF
≌△CBE．
求证：（1）∠A＝90°；
（2）四边形ABCD是矩形．
为了了解某区初中学生上学的交通方式，从中随机调查了300
0名学生的上学交通方式，统计结果如图所示．
（1）补全以上两幅统计图并标注相应数值；
（2）该区共有初中学生15000名，请估计其中骑自行上学的人数．
解方程：
－
＝1．