已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.
(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为N.
(ⅰ)若 ,求线段MN长度的取值范围;
(ⅱ)求△QMN面积的最小值.
如图,在平面直角坐标系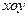 中,抛物线
中,抛物线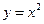 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线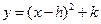 .所得抛物线与
.所得抛物线与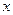 轴交于
轴交于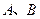 两点(点
两点(点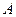 在点
在点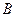 的左边),与
的左边),与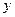 轴交于点
轴交于点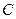 ,顶点为
,顶点为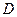 .
.
(1)求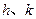 的值;
的值;
(2)求直线AC的函数解析式。
(3)在线段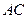 上是否存在点
上是否存在点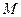 ,使
,使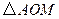 与
与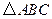 相似.若存在,求出点
相似.若存在,求出点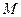 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.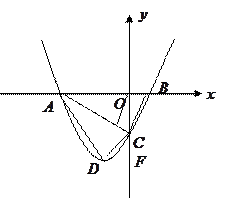
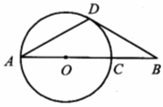
如图,线段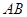 经过圆心
经过圆心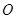 ,交⊙O于点
,交⊙O于点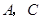 ,点
,点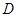 在⊙O上,连接
在⊙O上,连接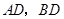 ,
,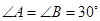 .
.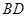 是⊙O的切线吗?请说明理由.
是⊙O的切线吗?请说明理由.
 |
(9分)如图,把△ABC置于平面直角坐标系中,请你按以下要求分别画图:
(1)画出△ABC向下平移5个单位长度得到的△A1B1C1;
(2)画出△ABC绕原点O逆时针旋转90º得到的△A2B2C2;
(3)画出△ABC关于原点O对称的△A3B3C3.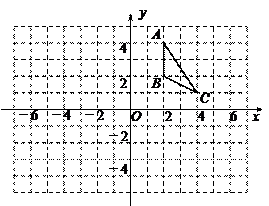
为了了解某校初中男生的身体素质状况,在该校六年级至九年级共四个年级的男生中,分别抽取部分学生进行“引体向上”测试.所有被测试者的“引体向上”次数情况如表一所示;各年级的被测试人数占所有被测试人数的百分率如图5所示(其中六年级相关数据未标出).
| 次数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 人数 |
1 |
1 |
2 |
2 |
3 |
4 |
2 |
2 |
2 |
0 |
1 |
表一
根据上述信息,回答下列问题(直接写出结果):
(1)六年级的被测试人数占所有被测试人数的百分率是
(2)在所有被测试者中,九年级的人数是 ;
(3)在所有被测试者中,“引体向上”次数不小于6的人数所占的百分率是 ;
(4)在所有被测试者的“引体向上”次数中,众数是
如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处。求此时渔船所在的B处与海洋观测站P的距离(结果保留根号)。