甲袋中装有4个相同的小球,分别标有3,4,5,6;乙袋中装有3个相同的小球,分别标有7,8,9.芳芳和明明用摸球记数的方法在如图所示的正六边形 ABCDEF的边上做游戏,游戏规则为:游戏者从口袋中随机摸出一个小球,小球上的数字是几,就从顶点 A按顺时针方向连续跳动几个边长,跳回起点者获胜;芳芳只从甲袋中摸出一个小球,明明先后从甲、乙口袋中各摸出一个小球.如:先后摸出标有4和7的小球,就先从点 A按顺时针连跳4个边长,跳到点 E,再从点 E顺时针连跳7个边长,跳到点 F.
分别求出芳芳、明明跳回起点 A的概率,并指出游戏规则是否公平.

如图,某文化广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB=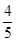 .
.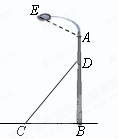
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
如图,一次函数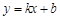 与反比例函数
与反比例函数 的图象交于A(2,1),B(-1,
的图象交于A(2,1),B(-1, )两点.
)两点.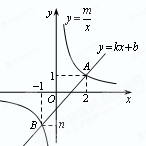
(1)求m、k、b的值;
(2)连接OA、OB,计算三角形OAB的面积;
(3)结合图象直接写出不等式 的解集.
的解集.
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率.
某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图10,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)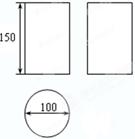
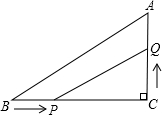
如图,△ABC中,∠C=90°,BC=8cm,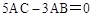 ,点P从B点出发,沿BC方向以2cm/m的速度移动,点Q从C出发,沿CA方向以1cm/m的速度移动。若P、Q同时分别从B、C出发,经过多少时间△CPQ与△CBA相似?
,点P从B点出发,沿BC方向以2cm/m的速度移动,点Q从C出发,沿CA方向以1cm/m的速度移动。若P、Q同时分别从B、C出发,经过多少时间△CPQ与△CBA相似?