在清江河污水网管改造建设中,需要确保在汛期来临前将建设过程中产生的渣土清运完毕,每天至少需要清运渣土12720m3,施工方准备每天租用大、小两种运输车共80辆.已知每辆大车每天运送渣土200m3,每辆小车每天运送渣土120m3,大、小车每天每辆租车费用分别为1200元,900元,且要求每天租车的总费用不超过85300元.
(1)施工方共有多少种租车方案?
(2)哪种租车方案费用最低,最低费用是多少?
解方程: .
如图,点 和点 是反比例函数 图象上的两点,一次函数 的图象经过点 ,与 轴交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,连接 , .已知 与 的面积满足 .
(1) , ;
(2)已知点 在线段 上,当 时,求点 的坐标.

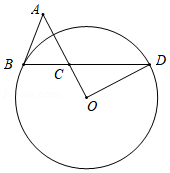
如图,在 中, ,过 延长线上的点 作 ,交 的延长线于点 ,以 为圆心, 长为半径的圆过点 .
(1)求证:直线 与 相切;
(2)若 , 的半径为12,则 .
如图,四边形 中, ,点 、 分别在 、 上, ,过点 、 分别作 的垂线,垂足为 、 .
(1)求证: ;
(2)连接 ,线段 与 是否互相平分?请说明理由.

如图,已知等边 的边长为8,点 是 边上的一个动点(与点 、 不重合).直线 是经过点 的一条直线,把 沿直线 折叠,点 的对应点是点 .
(1)如图1,当 时,若点 恰好在 边上,则 的长度为 ;
(2)如图2,当 时,若直线 ,则 的长度为 ;
(3)如图3,点 在 边上运动过程中,若直线 始终垂直于 , 的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当 时,在直线 变化过程中,求 面积的最大值.
