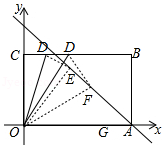
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线l:y=﹣x+7上时,记为点E,F,当点C的对应点落在边OA上时,记为点G.
(1)求点E,F的坐标;
(2)求经过E,F,G三点的抛物线的解析式;
(3)当点C的对应点落在直线l上时,求CD的长;
(4)在(2)中的抛物线上是否存在点P,使以E,F,P为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).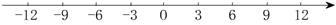
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
关于x的方程 与
与 的解互为相反数.
的解互为相反数.
(1)求m的值;
(2)求这两个方程的解.
两种移动电话记费方式表
(1)一个月内本地通话多少分钟时,两种通讯方式的费用相同?
(2)若某人预计一个月内使用本地通话费180元,则应该选择哪种通讯方式较合算?
| 全球通 |
神州行 |
|
| 月租费 |
50元/分 |
0 |
| 本地通话费 |
0.40元/分 |
0.60元/分 |
观察一列数:1、2、4、8、16、…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列5、-15、45、…的第4项是_________.
(2)如果一列数 是等比数列,且公比为
是等比数列,且公比为 .那么有:
.那么有: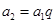 ,
, ,
, .则:
.则: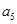 = .(用
= .(用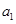 与
与 的式子表示)
的式子表示)
(3)一个等比数列的第2项是10,第4项是40,求它的公比.
统计数据显示,在我国的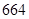 座城市中,按水资源情况可分为三类:暂不缺水城市、一般缺水城市和严重缺水城市.其中,暂不缺水城市数比严重缺水城市数的3倍多52座,一般缺水城市数是严重缺水城市数的
座城市中,按水资源情况可分为三类:暂不缺水城市、一般缺水城市和严重缺水城市.其中,暂不缺水城市数比严重缺水城市数的3倍多52座,一般缺水城市数是严重缺水城市数的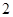 倍.求严重缺水城市有多少座?
倍.求严重缺水城市有多少座?