(·黑龙江绥化)自学下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如: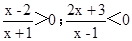 等 。那么如何求出它们的解集呢?
等 。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负。其字母表达式为:
(1)若a>0 ,b>0 ,则 >0;若a<0 ,b<0,则
>0;若a<0 ,b<0,则 >0;
>0;
(2)若a>0 ,b<0 ,则 <0 ;若a<0,b>0 ,则
<0 ;若a<0,b>0 ,则 <0。
<0。
反之:(1)若 >0则
>0则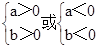
(2)若 <0 ,则__________或_____________.
<0 ,则__________或_____________.
根据上述规律,求不等式 的解集。
的解集。
为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,根据老年人、成年人、青少年各年龄段实际人口的比例3:5:2,随机抽取一定数量的观众进行调查,得到如下统计图.
(1)上面所用的调查方法是(填“全面调查”或“抽样调查”);
(2)写出折线统计图中A、B所代表的值; A:;B:;
(3)求该地区喜爱娱乐类节目的成年人的人数.
已知△ABC在平面直角坐标系中的位置如图所示.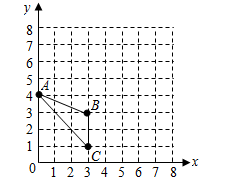
(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)求点A旋转到点A′所经过的路线长(结果保留π)
如图,二次函数y=- x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.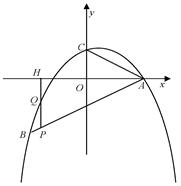
(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF 
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为 ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.
草梅是我地区的特色时令水果,草梅一上市,水果店的老板用1200元购进一批草梅,很快售完;老板又用2500元购进第二批草梅,所购箱数是第一批的2倍,但进价比第一批每箱多了5元.
(1)第一批草梅每箱进价多少元?
(2)老板以每箱150元的价格销售第二批草梅,售出80%后,为了尽快售完,决定打折促销,要使第二批草梅的销售利润不少于320元,剩余的草梅每箱售价至少打几折?(利润=售价﹣进价)