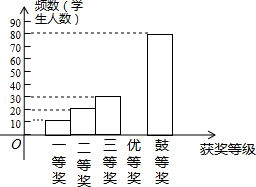
国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 |
频数 |
频率 |
一等奖 |
10 |
0.05 |
二等奖 |
20 |
0.10 |
三等奖 |
30 |
b |
优胜奖 |
a |
0.30 |
鼓励奖 |
80 |
0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
如图,在四边形ABCD中,点E、F是BC、CD的中点,且AE⊥BC,AF⊥CD.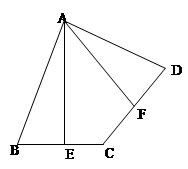
(1)求证:AB=AD.
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
(1)解方程:16(x+1)2 -1=0
(2)-(x-3)3=27
(3)先化简,再求值: ,其中
,其中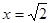 .
.
(4)实数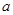 、
、 在数轴上的位置如图所示,请化简:
在数轴上的位置如图所示,请化简: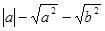 .
.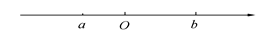
(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E .求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120º得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
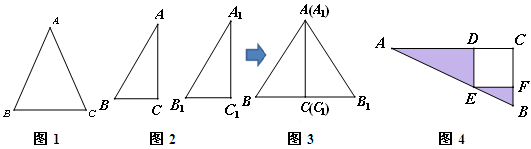
阅读理解:“分割、拼凑法”是几何证明中常用的方法。苏科版八上数学第一章《全等三角形》中,有以下两道题,其中问题1中的图1分割成两个全等三角形,而问题2是“HL定理”的证明,却将图2两个直角三角形拼成了一个等腰三角形图3.
请按照上面的思路,补全问题1、2的解答:
问题1:已知:如图1,在△ABC中,AB=AC.求证:∠B=∠C.
问题2:如图2,在△ABC和△A1B1C1中,∠C=∠C1=90°,AB=A1B1,AC=A1C1.
求证:△ABC≌△A1B1C1(补全证明过程) .
证明:把两个直角三角形如图3所示拼在一起.
仿照上面的方法解答问题:
问题3:如图4,△ABC中,∠ACB=90°,四边形CDEF是正方形,AE=5,BE=3.
求阴影部分的面积和.