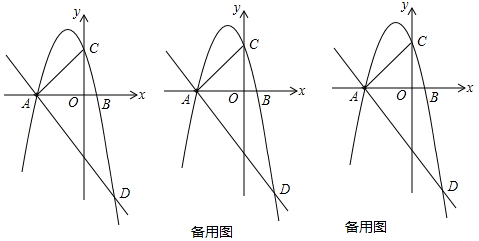
如图所示，已知抛物线 ，与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线 与抛物线的另一个交点为D．
（1）若点D的横坐标为2，求抛物线的函数解析式；
（2）若在第三象限内的抛物线上有点P，使得以A、B、P为顶点的三角形与△ABC相似，求点P的坐标；
（3）在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒 个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？
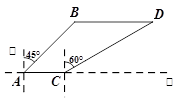
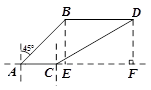
如图，港口B在港口A的东北方向，上午9时，一艘轮船从港口A出发，以16
海里/时的速度向正东方向航行，同时一艘快艇从港口B出发也向正东方向航行．上午11时轮船到达C处，同时快艇到达D处，测得D处在C处的北偏东60°的方向上，且C、D两地相距80海里，求快艇每小时航行多少海里？（结果精确到0.1海里/时，参考数据：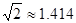
，
，
）
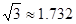去年寒假期间，学校团委要求学生参加一项社会调查活动，八年级学生小青想了解她所在的小区500户居民家庭月人均收入情况，从中随机调查了一定数量的居民家庭的月人均收入（元）情况，并绘制成如下的频数分布直方图（每组含左端点，不含右端点）和扇形统计图．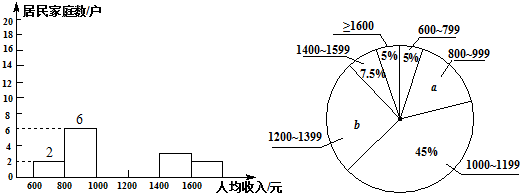
请你根据以上不完整的频数分布直方图和扇形统计图提供的信息，解答下列问题：这次共调查了多少户居民家庭的人均收入？扇形统计图中的a=，b= ；．
补全频数分布直方图．
如图，AB、BF分别是⊙O的直径和弦，弦CD与AB、BF分别相交于点E、G，过点F的切线HF与DC的延长线相交于点H，且HF＝HG.求证：AB⊥CD；
若sin∠HGF＝
，BF＝3，求⊙O的半径长.
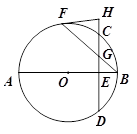
如图，四边形ABCD是矩形，AB=3，BC=4，把矩形沿直线AC折叠，点B落在点F处，连接DF，CF与AD相交于点E，求DE的长和△ACE的面积.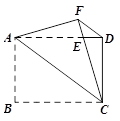
如图，点P（－3，1）是反比例函数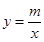
的图象上的一点.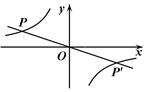
求该反比例函数的解析式；
设直线
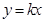与双曲线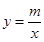的两个交点分别为P和P′，
当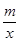
＜
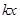时，直接写出x的取值范围．