去年寒假期间,学校团委要求学生参加一项社会调查活动,八年级学生小青想了解她所在的小区500户居民家庭月人均收入情况,从中随机调查了一定数量的居民家庭的月人均收入(元)情况,并绘制成如下的频数分布直方图(每组含左端点,不含右端点)和扇形统计图.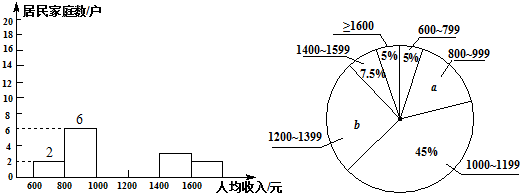
请你根据以上不完整的频数分布直方图和扇形统计图提供的信息,解答下列问题:这次共调查了多少户居民家庭的人均收入?扇形统计图中的a=,b= ;.
补全频数分布直方图.
如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 .
(1)求抛物线的解析式;
(2) 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;
(3) 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , ,探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.

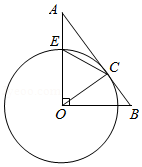
如图,在 中, , 与 相交于点 ,与 相交于点 ,连接 ,已知 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.
“互联网 ”让我国经济更具活力,直播助销就是运用“互联网 ”的生机勃勃的销售方式,让大山深处的农产品远销全国各地.甲为当地特色花生与茶叶两种产品助销.已知每千克花生的售价比每千克茶叶的售价低40元,销售50千克花生与销售10千克茶叶的总售价相同.
(1)求每千克花生、茶叶的售价;
(2)已知花生的成本为6元 千克,茶叶的成本为36元 千克,甲计划两种产品共助销60千克,总成本不高于1260元,且花生的数量不高于茶叶数量的2倍.则花生、茶叶各销售多少千克可获得最大利润?最大利润是多少?
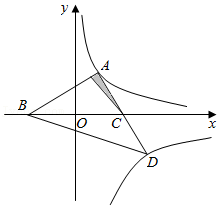
如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 .
(1)求 ;
(2)直线 与双曲线 在第四象限交于点 ,求 的面积.
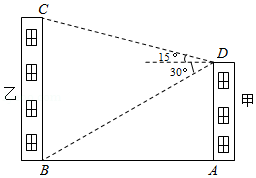
乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到