某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:

(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
用简便方法计算
(1)
(2)
分解因式:
(1)3a3-6a2+3a
(2)a2(x-y)+b2(y-x)
(3)16(a+b)2-9(a-b)2
如图,已知D是BC的中点,过点D作BC的垂线交∠A的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.求证:BF=CG.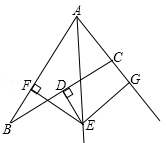
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).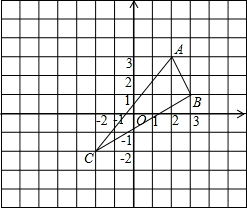
(1)请在图中作出△ABC关于y轴对称图形△DEF
(2)写出D、E、F的坐标。
已知如图(1):△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.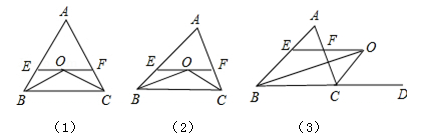
(1)写出线段EF与BE、CF间的数量关系?(不证明)
(2)若AB≠AC,其他条件不变,如图(2),图中线段EF与BE、CF间是否存在(1)中数量关系?请说明理由.
(3)若△ABC中,AB≠AC,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,如图(3),这时图中线段EF与BE,CF间存在什么数量关系?请说明理由.