如图,已知 BC⊥ AC,圆心 O在 AC上,点 M与点 C分别是 AC与⊙ O的交点,点 D是 MB与⊙ O的交点,点 P是 AD延长线与 BC的交点,且 = .
(1)求证: PD是⊙ O的切线;
(2)若 AD=12, AM= MC,求 的值.

我市某中学八年级实行小班教学,若每间教室安排20名学生,则缺少3间教室;若每间教室安排24名学生,则正好空出一间教室。问这个学校现有空教室多少间?八年级共有多少人?
有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ恰好分别经过点B、C.△ABC中,∠A=30°.
(1)如图1,则∠ABC+∠ACB=度,∠XBC+∠XCB=度;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
如图,在△ABC和△ADE中,已知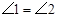 ,
,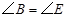 ,
,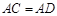 .请说明
.请说明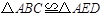 的理由.
的理由.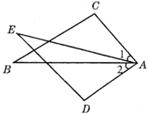
.如图:在正方形网格中有一个△ABC,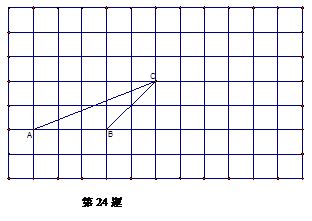
按要求进行下列作图(只能借助于网格):
(1)、画出△ABC中BC边上的高(需写出结论)。
(2)、画出先将△ABC向右平移6格,
再向上平移3格后的△DEF。
(3)、画一个锐角△MNP(要求各顶点在格点上),
使其面积等于△ABC的面积。
如图,AD⊥BD,AE平分∠BAD, ∠B=30°,
∠ACD=70°,求∠EAB和∠CAE的度数。