如图,抛物线 y= ax 2+ bx﹣2( a≠0)与 x轴交于 A(﹣3,0), B(1,0)两点,与 y轴交于点 C,直线 y=﹣ x与该抛物线交于 E, F两点.
(1)求抛物线的解析式.
(2) P是直线 EF下方抛物线上的一个动点,作 PH⊥ EF于点 H,求 PH的最大值.
(3)以点 C为圆心,1为半径作圆,⊙ C上是否存在点 M,使得△ BCM是以 CM为直角边的直角三角形?若存在,直接写出 M点坐标;若不存在,说明理由.

如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
(1)解方程:
(2)先化简,再求值: ,其中
,其中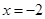 ,
, .
.
(本题14分)已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.
(1)问多少秒后,甲到A,B,C的距离和为40个单位?
(2)若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?
(3)在(1)(2)的条件下,当甲到A、B、C的距离和为40个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
(本题12分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+5 |
-2 |
-4 |
+13 |
-10 |
+16 |
-9 |
(1)根据记录可知前三天共生产辆;
(2)产量最多的一天比产量最少的一天多生产辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
(本题8分)先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解 1+2+3+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101×=.
(1)在上面横线上补全例题解题过程;
(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).