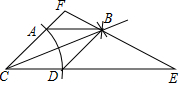
已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△ CFE中, CF=6, CE=12,∠ FCE=45°,以点 C为圆心,以任意长为半径作 ,再分别以点 A和点 D为圆心,大于 AD长为半径作弧,交 EF于点 B, AB∥ CD.
(1)求证:四边形 ACDB为△ FEC的亲密菱形;
(2)求四边形 ACDB的面积.
如图,已知 , ,抛物线 过 、 两点,并与过 点的直线 交于点 .
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点 ,使四边形 的周长最小?若存在,求出点 的坐标,若不存在,请说明理由;
(3)点 为 轴右侧抛物线上一点,过点 作直线 的垂线,垂足为 .问:是否存在这样的点 ,使以点 、 、 为顶点的三角形与 相似,若存在,求出点 的坐标,若不存在,请说明理由.

如图1,点 是正方形 边 上任意一点,以 为边作正方形 ,连接 ,点 是线段 中点,射线 与 交于点 ,连接 .
(1)请直接写出 和 的数量关系和位置关系;
(2)把图1中的正方形 绕点 顺时针旋转 ,此时点 恰好落在线段 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形 绕点 顺时针旋转 ,此时点 、 恰好分别落在线段 、 上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.

鹏鹏童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖10件.已知该款童装每件成本30元.设该款童装每件售价 元,每星期的销售量为 件.
(1)求 与 之间的函数关系式(不求自变量的取值范围);
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少?
(3)①当每件童装售价定为多少元时,该店一星期可获得3910元的利润?
②若该店每星期想要获得不低于3910元的利润,则每星期至少要销售该款童装多少件?
如图,在 中, ,点 在线段 上,以 为直径的 与 相交于点 ,与 相交于点 , .
(1)求证: 是 的切线;
(2)若 ,求 的半径 ;
(3)在(1)的条件下,判断以 、 、 、 为顶点的四边形为哪种特殊四边形,并说明理由.

东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于 ,那么每套悠悠球的售价至少是多少元?