某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元．
（1）第一批饮料进货单价多少元？
（2）若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？
如图，某高速公路建设中需要确定隧道AB的长度．已知在离地面1500m高度C
处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°．求隧道AB的长
(
≈1.73)．
在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方
向依次不断移动，每次移动1个单位，其行走路线如下图所示．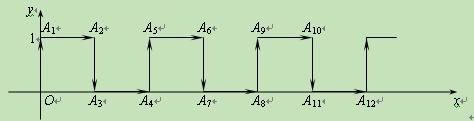
(1)填写下列各点的坐标：A4(，)、A8(，)、A12(，)；
(2)写出点A4n的坐标(n是正整数)；
(3)指出蚂蚁从点A100到点A101的移动方向．
如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1
和△A2B2C2：
(1)将△ABC先向右平移4个单位，再向上平移1个单位，得到△A1B1C1；
(2)以图中的点O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2．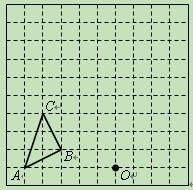
江南生态食品加工厂收购了一批质量为10000kg的某种山货，根据市场需求对其
进行粗加工和精加工处理，已知精加的这种山货质量比粗加工的质量的3倍还多2000kg，
求粗加工的这种山货的质量．
先化简，再求值：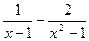
，其中x＝－2．