如图1，在△ ABC中， AB＝ AC，⊙ O是△ ABC的外接圆，过点 C作∠ BCD＝∠ ACB交⊙ O于点 D，连接 AD交 BC于点 E，延长 DC至点 F，使 CF＝ AC，连接 AF．
（1）求证： ED＝ EC；
（2）求证： AF是⊙ O的切线；
（3）如图2，若点 G是△ ACD的内心， BC• BE＝25，求 BG的长．
某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图．根据图中提供的信息，解答下列问题：
（1）补全频数分布直方图；
（2）求扇形统计图中m的值和“E”组对应的圆心角度数；
（3）请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数．
解方程： 
= 
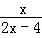﹣1．
化简：（
+
）÷ 
．
(1)有甲、乙、丙三种商品，如果购甲3件、乙2件、丙1件共需15元，如果购甲1件、乙2件、丙3件共需25元，那么购甲、乙、丙各1件共需多少元？
（2）已知2a+b+3c=15，3a+b+5c=25，则a+b+c=
（3）已知2a+b+xc=15，3a+b+yc=25， 要想求出a+b+c的值，x与y必须满足的关系是？
(10分)如图，四边形
中，
，
平分
交
于
，
平分
交
于
．
（1）若
，则
°，
°；
（2）求证：BE∥DF