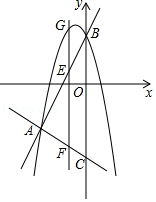
如图，抛物线y＝﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC： 交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．
（1）求抛物线y＝﹣x2+bx+c的表达式；
（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；
（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；
②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求 AM+CM它的最小值．
如图，在平面直角坐标系中，已知点
，反比例函数
的图像经过点A，动直线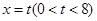
与反比例函数的图像交于点M，与直线AB交于点N．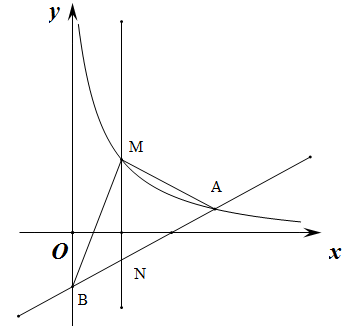
（1）求k的值；
（2）求△BMN面积的最大值；
（3）若
,求t的值．
如图，四边形ABCD中，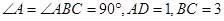
,E是边CD的中点，连接BE并延长与AD的延长线相较于点F．
（1）求证：四边形BDFC是平行四边形；
（2）若△BCD是等腰三角形，求四边形BDFC的面积．
如图，观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上，从点A处测得楼顶端B的仰角为22°，此时点E恰好在AB上，从点D处测得楼顶端B的仰角为38．5°．已知旗杆DE的高度为12米，试求楼房CB的高度．
（参考数据：sin22°≈0．37，cos22°≈0．93，tan22°≈0．40，sin38．5°≈0．62，cos38．5°≈0．78，tan38．5°≈0．80）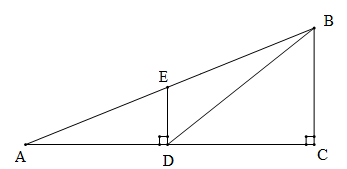
如图，已知
．
求证：
．
某校为了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组
（A:39．5~46．5;B:46．5~53．5;C:53．5~60．5;D:60．5~67．5;E:67．5~74．5），并依据统计数据绘制了如下两个不完整的统计图．
解答下列问题：
（1）这次抽样调查的样本容量是，并不全频数分布直方图；
（2）C组学生的频率为，在扇形统计图中D组的圆心角是度；
（3）请你估计该校初三年级体重超过60kg的学生大约有多少名？