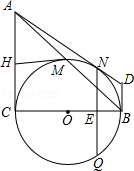
如图,在Rt△ ABC中,∠ C=90°,以 BC为直径的⊙ O交斜边 AB于点 M,若 H是 AC的中点,连接 MH.
(1)求证: MH为⊙ O的切线.
(2)若 ,求⊙ O的半径.
(3)在(2)的条件下分别过点 A、 B作⊙ O的切线,两切线交于点 D, AD与⊙ O相切于 N点,过 N点作 NQ⊥ BC,垂足为 E,且交⊙ O于 Q点,求线段 NQ的长度.
(本小题满分8分)
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇形内).请你用列表法或树状图求a与 b的乘积等于2的概率.
(本小题满分7分)
⑴计算: +
+
⑵如图所示,△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,若AC= .
.
求线段AD的长.
(本小题满分7分)
⑴解不等式组:
⑵如图所示,在梯形ABCD中,BC∥AD,AB=DC,点M是AD的中点.
求证:BM=CM.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3 ).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1,
).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查,速度分别为1, ,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
,2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以 (长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
请解答下列问题:
(1)过A,B两点的直线解析式是 ▲;
(2)当t﹦4时,点P的坐标为 ▲;当t ﹦ ▲,点P与点E重合;
(3)
① 作点P关于直线EF的对称点P′. 在运动过程中,若形成的四边形PEP′F为菱形,则t的值是多少?
② 当t﹦2时,是否存在着点Q,使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标;
若不存在,请说明理由.
已知点P的坐标为
,在
轴上存在点
(不与
点重合),以
为边作正方形
,使点
落在反比例函数
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点
在第四象限,另一个正方形的顶点
在第二象限.
(1)如图所示,若反比例函数解析式为
,
点坐标为
,图中已画出一符合条件的一个正方形
,请你在图中画出符合条件的另一个正方形
,并写出点
的坐标;
(温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!)
M1的坐标是 ▲
(2) 请你通过改变P点坐标,对直线M1 M的解析式
进行探究可得 k﹦,若点
的坐标为
时,则b﹦;
(3) 依据(2)的规律,如果点P的坐标为
,请你求出点M1和点M的坐标.