如图1，矩形ABCD中， ， ，点E为AD上一定点，点F为AD延长线上一点，且 ，点P从A点出发，沿AB边向点B以2cm/s的速度运动，连结PE，设点P运动的时间为ts，△PAE的面积为ycm2，当 时，△PAE的面积y（cm2）关于时间t（s）的函数图象如图2所示，连结PF，交CD于点H．
（1）t的取值范围为 ，AE＝ cm；
（2）如图3，将△HDF沿线段DF进行翻折，与CD的延长线交于点M，连结AM，当a为何值时，四边形PAMH为菱形？并求出此时点P的运动时间t；
（3）如图4，当点P出发1s后，AD边上另一动点Q从E点出发，沿ED边向点D以1cm/s的速度运动，如果P，Q两点中的任意一点到达终点后，另一点也停止运动，连结PQ，QH．若 ，请问△PQH能否构成直角三角形？若能，请求出点P的运动时间t；若不能，请说明理由．
右图是平面直角坐系: (6分)
(1)请写出
三个顶点的坐标.
(2)请画出向右平稳3个单位,再向下平移2个位所得到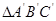
.
为了了解某校700名七年级新生入学时的数学水平，随机抽取若干名学生的数学成绩统计整理后绘制如图的频数分布直方图(分数取整数)，观察图形回答下列问题：
(1)79～89的频数是______________. (2分)
（2）本次随机抽查的学生人数是多少人. (2分)
（3）被抽取的人数中有多少人不格. (2分)
（4）你能否估计一下700名七年级学生成绩不有格的有多少人? (2分)
解下列不等式及不等式组,并把解集在数轴上表示出来.(每题4分,共8分)
(1) 3(2x+5)>2(4x+3)
(2)
解方程组(每小题4分,共8分)
(1)
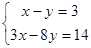
(2)
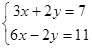
如图，在正方形ABCD中，E是AB边上任意一点，BG⊥CE，垂足为点O,交AC于点F，交AD于点G。
（1）证明：BE="AG" ；
（2）点E位于什么位置时，∠AEF=∠CEB，说明理由。