如图,已知抛物线 经过A(﹣3,0)、B(5,0)、C(0,5)三点,O为坐标原点.
(1)求此抛物线的解析式;
(2)若把抛物线 向下平移 个单位长度,再向右平移 个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足 ,求CP的长.

如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.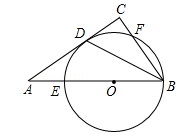
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
如图,以点P 为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=
为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=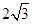 ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
如图,在直角坐标系中,A(0,4)、C(3,0),
(1)①画出线段AC关于y轴对称线段AB;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
如图1,四边形ABCD是边长为 的正方形,长方形AEFG的宽
的正方形,长方形AEFG的宽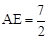 ,长
,长 .将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.
.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH (如图2),这时BD与MN相交于点O.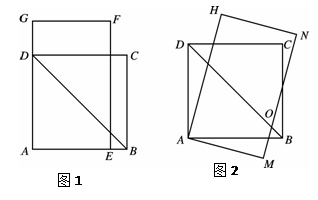
(1)求 的度数;
的度数;
(2)在图2中,求D、N两点间的距离;
(3)若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ,请问此时点B在矩形ARTZ的内部、外部、还是边上?并说明理由.