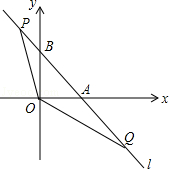
如图，直线 与x轴，y轴分别交于A，B两点，点P，Q是直线l上的两个动点，且点P在第二象限，点Q在第四象限， ．
（1）求△AOB的周长；
（2）设 ，试用含t的代数式表示点P的坐标；
（3）当动点P，Q在直线l上运动到使得△AOQ与△BPO的周长相等时，记 ，若过点A的二次函数 同时满足以下两个条件：
① ；
②当 时，函数y的最大值等于 ，求二次项系数a的值．
如图1，将底面为正方形的两个完全相同的长方体铁块放入一圆柱形水槽内，并向水槽内匀速注水，速度为v cm3/s，直至水面与长方体顶面平齐为止．水槽内的水深h（cm）与注水时间t（s）的函数关系如图2所示．根据图象完成下列问题：
（1）一个长方体的体积是cm3；
（2）求图2中线段AB对应的函数关系式；
（3）求注水速度v和圆柱形水槽的底面积S．
如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB＝4米，AC＝3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．
⑴ 在如图⑵建立的坐标系下，求网球飞行路线的抛物线解析式.
⑵ 若竖直摆放5个圆柱形桶时，则网球能落入桶内吗？说明理由；
⑶若要使网球能落入桶内，求竖直摆放的圆柱形桶的个数.
如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD="40" m，某人在河岸MN的A处测得∠DAN = 35°，然后沿河岸走了100 m到达B处，测得∠CBN=70°．求河流的宽度CE (精确到1m)．（参考数据： sin35°≈ 0.57, cos35°≈ 0.82,
tan35°≈ 0.70；sin 70°≈ 0.94, cos70°≈ 0.34, tan70°≈ 2.75）.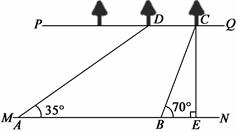
如图，在△ABO中，OA＝OB，C是边AB的中点，以O为圆心的圆过点C，且与OA交于点E、与OB交于点F，连接CE、CF．
⑴ 求证：AB是⊙O的切线；
⑵ 若∠AOB＝∠ECF，试判断四边形OECF的形状，并说明理由．
在如图的方格纸中，每个小方格都是边长为1个单位的正方形，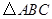
的三个顶点 都在格点上（每个小方格的顶点叫格点）．
⑴ 画出△ABC关于点O的中心对称的△A1B1C1；
⑵ 如果建立平面直角坐标系，使点B的坐标为（－5，2），点C的坐标为（－2，2），则点A1的坐标为；
⑶ 将△ABC绕点O顺时针旋转90°，画出旋转后的△A2B2C2，并求线段BC扫过的面积.