在学习完“利用三角函数测高”这节内容之后，某兴趣小组开展了测量学校旗杆高度的实践活动，如图，在测点 处安置测倾器，量出高度 ，测得旗杆顶端 的仰角 ，量出测点 到旗杆底部 的水平距离 ，根据测量数据，求旗杆 的高度．（参考数据： ， ，
（本题10分）如图，△ABC中，∠A=90º，∠ABC与∠ACB的角平分线交于点I，△ABC的外角∠DBC与∠BCE的角平分线交于P。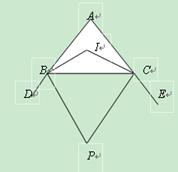
①则∠BIC= ，∠P= （直接写出答案）
②当∠A的度数增加4º时，∠BIC，∠P的度数发生怎样的变化？请说明理由。
（本题8分）如图，已知在四边形ABCD中，∠B=∠D=
，AE、CF分别是∠DAB及∠DCB的平分线．则AE与FC有什么关系？请说明理由。
（本题8分）在一个五边形ABCDE的每个顶点处各有一个以顶点为圆心，以2cm为半径的圆，每个圆与五边形重合的部分为图中阴影部分。求图中阴影部分的面积之和（答案用含有
的式子表示）。
（本题8分）在平面直角坐标系中,顺次连接A(-2,1),B(-2,-1),C(2,-2),D(2,3) ，A(-2,1)各点,你会得到一个什么图形?试求出该图形的面积.
（本题6分）如图，已知∠1 =∠2，∠B =∠C，可推得AB∥CD。
理由如下：
∵∠1 =∠2（已知），
且∠1 =∠CGD（__________________________）
∴∠2 =∠CGD（等量代换）
∴CE∥BF（_______________________________）
∴∠=∠BFD（__________________________）
又∵∠B =∠C（已知）
∴∠BFD =∠B（）
∴AB∥CD（________________________________）