如图①, 中, , 于点 ,点 在 上,且 ,连接 .
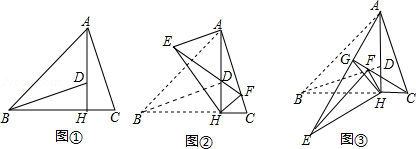
(1)求证: ;
(2)将 绕点 旋转,得到 (点 , 分别与点 , 对应),连接 .
①如图②,当点 落在 上时, 不与 重合),若 , ,求 的长;
②如图③,当 是由 绕点 逆时针旋转 得到时,设射线 与 相交于点 ,连接 ,试探究线段 与 之间满足的等量关系,并说明理由.
你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点 上下转动,立柱
上下转动,立柱 与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的过程中,两人上升的最大高度
与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的过程中,两人上升的最大高度 ,
, 有何数量关系?为什么?
有何数量关系?为什么?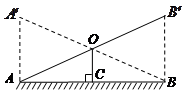
已知:如图, 是
是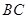 的中点,
的中点, ,
, .
.
求证: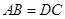 .
.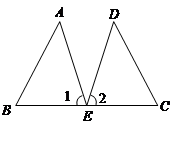
小明、小敏两人一起做数学作业,小敏把题读到如图8(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说: “这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明说:“小敏你错了,你未弄清本题的条件和结论,即使有CD⊥AB,BE⊥AC,公共角∠DAC=∠BAE,你的推理也是错误的.看我画的图8(2),显然△DAC与△EAB是不全等的.再说本题不是要证明∠B=∠C,而是要证明BE=CD.”根据小敏所读的题,判断“∠B=∠C”对吗?她的推理对吗?若不对,请做出正确的推理.
根据小明说的,要证明BE=CD,必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD的正确推理.
要判断三角形全等,从这个问题中你得到了什么启发?
飞翔建筑公司在扩建二汽修建厂房时,在一空地上发现有一个较大的圆形土丘,经分析判断很可能是一座王储陵墓,由于条件限制,无法直接度量A、B两点间的距离,请你用学过的数学知识,按以下要求设计测量方案.画出测量方案;
写出测量步骤(测量数据用字母表示);
计算AB的距离(写出求解或推理过程,结果用字母表示).

如图,要测量河两岸相对的两点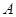 ,
,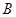 的距离,可以在
的距离,可以在 的垂线
的垂线 上取两点
上取两点 ,使
,使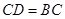 ,再定出
,再定出 的垂线
的垂线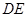 ,使
,使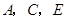 在一条直线上,这时测得的
在一条直线上,这时测得的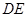 的长就是
的长就是 的长,为什么?
的长,为什么?