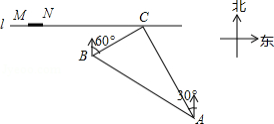
如图,在一条笔直的东西向海岸线 上有一长为 的码头 和灯塔 ,灯塔 距码头的东端 有 .一轮船以 的速度航行,上午 在 处测得灯塔 位于轮船的北偏西 方向,上午 在 处测得灯塔 位于轮船的北偏东 方向,且与灯塔 相距 .
(1)若轮船照此速度与航向航行,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据: ,
化简求值.
已知a,b满足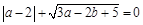 ,求代数式
,求代数式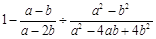 的值.
的值.
解分式方程.
(1) 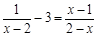 (2)
(2) 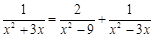
如图,在△ABC中,BD、CD是内角平分线,BP、CP是∠ABC、∠ACB的外角平分线,分别交于D、P.
(1)若∠A = 30°,求∠BDC和∠BPC的度数.
(2)不论∠A怎样变化,探索∠BDC +∠BPC的值是否有所变化?请说明理由.
列方程组解下列应用题.(每小题8分,共16分)
(1)甲、乙两人分别以均匀的速度在400米圆形跑道上跑步,甲的速度较快.当两人反向跑时,每40秒钟相遇一次;当两人同向跑时,每3分20秒相遇一次,求甲、乙两人的速度.
(2)某市政府决定2012年投入6000万元用于改善医疗卫生服务,比2011年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2012年投入“需方”的资金比2011年提高30%,投入“供方”的资金将比2011年提高20%.该市政府2011年投入“需方”和“供方”的资金各是多少万元?
如图,已知∠1 +∠2 =180°,∠DEF =∠A,求证:∠ACB = ∠DEB.