如图,已知抛物线 交 轴与 , 两点(点 在点 左侧),将直尺 与 轴负方向成 放置,边 经过抛物线上的点 ,与抛物线的另一交点为点 ,直尺被 轴截得的线段 ,且 的面积为6.
(1)求该抛物线的解析式;
(2)探究:在直线 上方的抛物线上是否存在一点 ,使得 的面积最大?若存在,请求出面积的最大值及此时点 的坐标;若不存在,请说明理由.
(3)将直尺以每秒2个单位的速度沿 轴向左平移,设平移的时间为 秒,平移后的直尺为 ,其中边 所在的直线与 轴交于点 ,与抛物线的其中一个交点为点 ,请直接写出当 为何值时,可使得以 、 、 、 为顶点的四边形是平行四边形.

某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图.(近视程度分为轻度、中度、高度三种)
(1)求这1000名小学生患近视的百分比.
(2)求本次抽查的中学生人数.
(3)该市有中学生8万人,小学生10万人.分别估计该市的中学生与小学生患“中度近视”的人数.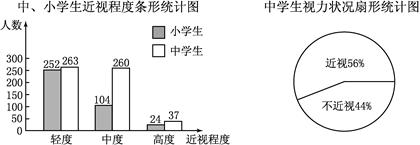
如图,点P的坐标为(2,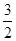 ),过点P作x轴的平行线交y轴于点A,交双曲线
),过点P作x轴的平行线交y轴于点A,交双曲线 (x>0)于点N;作PM⊥AN交双曲线
(x>0)于点N;作PM⊥AN交双曲线 (x>0)于点M,连结AM.已知PN=4.
(x>0)于点M,连结AM.已知PN=4.
(1)求k的值.
(2)求△APM的面积.
地的距离为18千米.一次行动中,王警官带队从O地出发,沿OC方向行进.王警官与指挥中心均配有对讲机,两部对讲机只能在10千米之内进行通话.通过计算判断王警官在行进过程中能否实现与指挥中心用对讲机通话.
【参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73.】
图①、图②均为7×6的正方形网格,点A、B、C在格点上.
(1)在图①中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为轴对称图形.(画一个即可)
(2)在图②中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为中心对称图形.(画一个即可)
某工程队承接了3000米的修路任务,在修好600米后,引进了新设备,工作效率是原来的2倍,一共用30天完成了任务.求引进新设备前平均每天修路多少米.