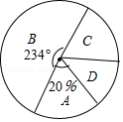
某中学为了科学建设“学生健康成长工程”，随机抽取了部分学生家庭对其家长进行了主题“周末孩子在家您关心了吗？”的调查问卷，将收回的调查问卷进行了分析整理，得到了如下的样本统计图表和扇形统计图：
代号 |
情况分类 |
家庭数 |
|
带孩子玩且关心其作业完成情况 |
8 |
|
只关心其作业完成情况 |
|
|
只带孩子玩 |
4 |
|
既不带孩子玩也不关心其作业完成情况 |
|
（1）求 ， 的值；
（2）该校学生家庭总数为500，学校决定按比例在 、 、 类家庭中抽取家长组成培训班，其比例为 类 ， 、 类各取 ，请你估计该培训班的家庭数；
（3）若在 类家庭中只有一个是城镇家庭，其余是农村家庭，请用列举法求出 类中随机抽出2个家庭进行深度家访，其中有一个是城镇家庭的概率．
如图，直线
与
轴负半轴、
轴正半轴分别交于A、B两点，正比例函数
的图像与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM =10，BN =3，
（1）求A、B两点的坐标；（用b表示）
（2）图中有全等的三角形吗？若有，请找出并说明理由。
（3）求MN的长．
下面是某同学对多项式
进行因式分解的过程.
解：设
原式=
（第一步）
=
（第二步）
=
（第三步）
=
（第四步）
请问：
（1）该同学因式分解的结果是否彻底？____________.(填“彻底”或“不彻底”)
若不彻底，请直接写出因式分解的最后结果____________________________
（2）请你模仿以上方法尝试对多项式
进行因式分解.
小聪和小明沿同一条路同时从学校出发到图书馆查阅资料，学校与图书馆的路程是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线O－A－B－C和线段OD分别表示两人离学校的路程
（千米）与所经过的时间
（分钟）之间的函数关系，请根据图象回答下列问题：
（1）小聪在图书馆查阅资料的时间为分钟，小聪返回学校的速度为千米/分钟．
（2）请你求出小明离开学校的路程(千米)与所经过的时间(分钟)之间的函数关系；
（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
如图，AD是ΔABC的角平分线，DE
AB，DFAC，垂足分别是点E，F，连结EF，交AD于点G，求证：AD⊥EF
如图，A，B两点的坐标分别是（2，
），（3，0）
（1）求△OAB的面积；
（2）将△OAB向下平移个单位，画出平移后的图形，并写出所得的三角形的三个顶点的坐标。