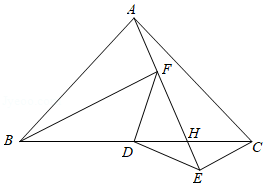
(本题满分12分)在四边形ABCD中,AD=a,CD=b,点E在射线BA上,点F在射线BC上.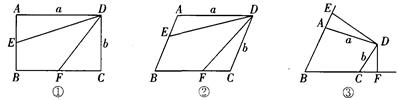
观察计算:
(1)如图①,若四边形ABCD是矩形,E是AB的中点.F是BC的中点,则四边形DEBF 的面积S四边形DEBF=_______.
(2)若四边形ABCD是平行四边形,E是AB的中点,F是BC的中点,则S四边形DEBF:S四边形ABCD=_______.
(3)如图②,若四边形ABCD是平行四边形,且BE:AB=2:3,BF:BC=2:3,则S四边形DEBF:S四边形ABCD=_______.
探索规律:
如图③,在四边形ABCD中,若BE:AB=n:m,BF:BC=n:m,试猜想S四边形DEBF:S四边形ABCD=_______,请说明理由.
解决问题:
如图④,某小区角落有一四边形空地,为了充分利用空间,美化环境,想把它沿两侧墙壁改造为一块绿地,使绿地面积是原空地面积的3倍.请分别在两侧墙壁上确定点E、F,画出改造线DE、DF,并写出作法.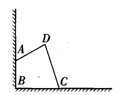
某学校九年级有12个班,每班50名学生,为了调查该校九年级学生平均每天的睡眠时间,准备从12个班里抽取50名学生作为一个样本进行分析,并规定如下:设每个学生平均每天的睡眠时间为 (单位,小时),将收集到的学生平均每天睡眠时间按 、 、 分为三类进行分析.
(1)下列抽取方法具有代表性的是 .
.随机抽取一个班的学生
.从12个班中,随机抽取50名学生
.随机抽取50名男生
.随机抽取50名女生
(2)由上述具有代表性的抽取方法抽取50名学生,平均每天的睡眠时间数据如表:
|
睡眠时间 (小时) |
5 |
5.5 |
6 |
6.5 |
7 |
7.5 |
8 |
8.5 |
|
人数(人 |
1 |
1 |
2 |
10 |
15 |
9 |
10 |
2 |
①这组数据的众数和中位数分别是 , ;
②估计九年级学生平均每天睡眼时间 的人数大约为多少;
(3)从样本中学生平均每天眠时间 的4个学生里,随机抽取2人,画树状图或列表,求抽得2人平均每天睡眠时间都是6小时的概率.
如图,在 中, ,点 是斜边 上一点,且 .
(1)作 的平分线,交 于点 ;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 ,求证: .

先化简,再求值: ,其中 .
如图,在平面直角坐标系 中,抛物线 过点 , ,点 为第二象限抛物线上一点,连接 , , ,其中 与 轴交于点 ,且 .
(1)求点 坐标;
(2)点 为线段 上一动点 不与 , 重合),过点 作平行于 轴的直线 与 的边分别交于 , 两点,将 沿直线 翻折得到△ ,设四边形 的面积为 ,在点 移动过程中,求 与 的函数关系式;
(3)在(2)的条件下,若 ,请写出所有满足条件的 值.

如图, 和 都是等腰直角三角形, , , , , 为 边中点,连接 ,且 、 、 三点恰好在一条直线上, 交 于点 ,连接 , .
(1)求证: ;
(2)猜想 , , 之间的数量关系,并证明;
(3)若 , ,请写出线段 , 的长.