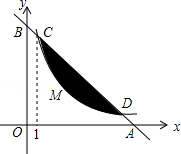
如图，直线 与 轴交于点 ，与 轴交于点 ，与反比例函数 的图象在第一象限交于 、 两点，点 为坐标原点， 的面积为 ，点 横坐标为1．
（1）求反比例函数的解析式；
（2）如果一个点的横、纵坐标都是整数，那么我们就称这个点为“整点”，请求出图中阴影部分（不含边界）所包含的所有整点的坐标．
化简：
.
在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE＝
∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．
（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；
（2）通过观察、测量、猜想：
=，并结合图②证明你的猜想；
（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求的值．（用含α的式子表示）
已知直线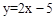
与x轴和y轴分别交于点A和点B，抛物线
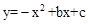的顶点M在直线AB上，且抛物线与直线AB的另一个交点为N．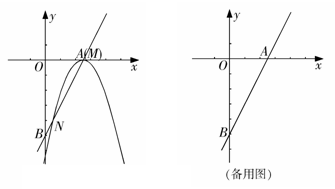
（1）如图，当点M与点A重合时，求：
①抛物线的解析式；
②点N的坐标和线段MN的长；
（2）抛物线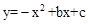在直线AB上平移，是否存在点M，使得△OMN与△AOB相似？若存在，直接写出点M的坐标；若不存在，请说明理由．
如图，在△ABC中，点O在AB上，以O为圆心的圆经过A，C两点，交AB于点D，已知∠A=α，∠B=β，且2α＋β=900．
（1）求证：BC是⊙O的切线；
（2）若OA=6，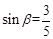
，求BC的长．
某商店销售A，B两种商品，已知销售一件A种商品可获利润10元，销售一件B种商品可获利润15元．
（1）该商店销售A，B两种商品共100件，获利润1350元，则A，B两种商品各销售多少件？
（2）根据市场需求，该商店准备购进A，B两种商品共200件，其中B种商品的件数不多于A种商品
件数的3倍．为了获得最大利润，应购进A，B两种商品各多少件？可获得最大利润为多少元？