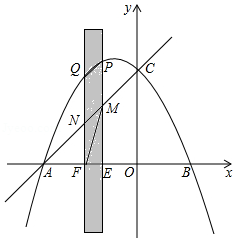
如图,抛物线与 轴交于点 和点 .与 轴交于点 .有一宽度为1,长度足够的矩形(阴影部分)沿 轴方向平移,与 轴平行的一组对边交抛物线于点 和 ,交直线 于点 和 .交 轴于点 和 .
(1)求抛物线的解析式;
(2)当点 和 都在线段 上时,连接 ,如果 ,求点 的坐标;
(3)在矩形的平移过程中,当以点 , , , 为顶点的四边形是平行四边形时,求点 的坐标.
10袋小麦以每袋150千克为标准,超过150千克的部分记为正数,不足150千克的部分记为负数,记录情况如下表:
| 编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 差值/kg |
-6 |
-3 |
-1 |
+7 |
+3 |
+4 |
-3 |
-2 |
-2 |
+1 |
(1)与标准重量相比较,10袋小麦总计超过或不足多少千克?
(2)每袋小麦的平均重量是多少千克?
化简或求值
(1)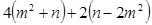 (2)
(2)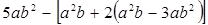

(3) 已知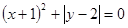 。求
。求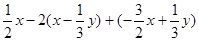 的值.
的值.
(4)如果代数式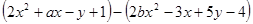 的值与字母x所取的值无关,试求代数式
的值与字母x所取的值无关,试求代数式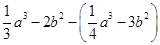 的值
的值
计算题 (2)
(2)
 (4)
(4)
如图,已知 ,
, 是一次函数
是一次函数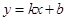 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线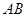 与
与 轴的交点
轴的交点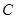 的坐标及△
的坐标及△ 的面积;
的面积;
(3)求不等式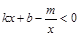 的解集(请直接写出答案).
的解集(请直接写出答案).
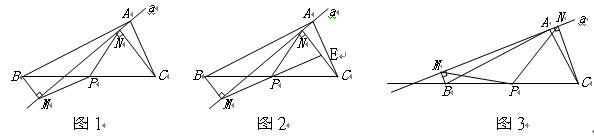
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM^直线a于点M,CN^直线a于点N,连接PM、PN;
(1) 延长MP交CN于点E(如图2)。j求证:△BPM≌△CPE;k求证:PM=PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时
PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。