如图，在RtΔABC中，∠ABC90°，AC的垂直平分线分别-优题课

题文

如图，在 $Rt Δ ABC$ 中， $∠ ABC = 90 °$ ， $AC$ 的垂直平分线分别与 $AC$ ， $BC$ 及 $AB$ 的延长线相交于点 $D$ ， $E$ ， $F$ ， $⊙ O$ 是 $ΔBEF$ 的外接圆， $∠ EBF$ 的平分线交 $EF$ 于点 $G$ ，交 $⊙ O$ 于点 $H$ ，连接 $BD$ 、 $FH$ ．

（1）试判断 $BD$ 与 $⊙ O$ 的位置关系，并说明理由；

（2）当 $AB = BE = 1$ 时，求 $⊙ O$ 的面积；

（3）在（2）的条件下，求 $HG \cdot HB$ 的值．

科目数学题型解答题难度中等

知识点：圆周角定理相似三角形的判定与性质三角形的外接圆与外心直线与圆的位置关系全等三角形的判定与性质线段垂直平分线的性质直角三角形的性质

登录免费查看答案和解析

相关试题

⑴计算：；
⑵解方程：.

平面内的两条直线有相交和平行两种位置关系（本题6分）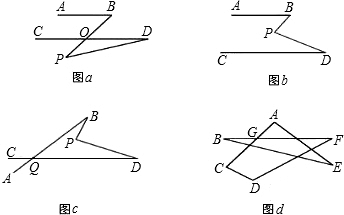

（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B-∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明理由；
（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需说明理由）
（3）求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．（简述理由）

如图：用两个边长为a、b、c的直角三角形和一个边长为c的等腰直角三角形拼成一个直角梯形，试用不同的方法计算这个图形的面积。（本题6分）

（1）你能得到关于a，b，c的一个等式吗？写出你的过程。
（2）请用一句话描述你的发现：在直角三角形中，
（3）请应用你学到的新知识解决下面这个问题：将一根长为30cm的筷子置于底面直径为5cm，高12cm的圆柱形的空水杯中，则露出杯子外面的长度最短是____cm ,最长是____ cm.如果把圆柱体换成一个长，宽，高分别为6,8,24的无盖长方体盒子。那么这根筷子露出盒子外面的长度最短是____cm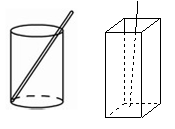

如图，AD为△ABC的中线，BE为△ABD的中线。解决下列问题（本题5分）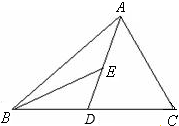

（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；
（2）作△BED中BD边上的高EF；
（3）若△ABC的面积为40，BD=5，则△BDE中BD边上的高EF为多少？

已知：与的和为零,先化简再求值：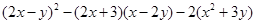
（本题4分）

试卷网试题网古诗词网作文网范文网