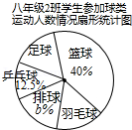
某校要求八年级同学在课外活动中，必须在五项球类（篮球、足球、排球、羽毛球、乒乓球）活动中任选一项（只能选一项）参加训练，为了了解八年级学生参加球类活动的整体情况，现以八年级2班作为样本，对该班学生参加球类活动的情况进行统计，并绘制了如图所示的不完整统计表和扇形统计图：
八年级2班参加球类活动人数统计表 |
|||||
项目 |
篮球 |
足球 |
乒乓球 |
排球 |
羽毛球 |
人数 |
|
6 |
5 |
7 |
6 |
根据图中提供的信息，解答下列问题：
（1） ， ；
（2）该校八年级学生共有600人，则该年级参加足球活动的人数约 人；
（3）该班参加乒乓球活动的5位同学中，有3位男同学 ， ， 和2位女同学 ，现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．
已知：如图，在梯形ABCD中，AD // BC，AB⊥BC，点M在边BC上，且∠MDB =∠ADB，
．
（1）求证：BM=CM；
（2）作BE⊥DM，垂足为点E，并交CD于点F．
求证：
．
如图，在平行四边形ABCD中，点E在边BC上，联结AE并延长，交对角线BD于点F、DC的延长线于点G，如果
．
求
的值．
某条道路上通行车辆限速为60千米/时，在离道路50米的点P处建一个监测点，道路的AB段为监测区（如图）．在△ABP中，已知∠PAB = 32º，∠PBA = 45º，那么车辆通过AB段的时间在多少秒以内时，可认定为超速（精确到0.1秒）？
（参考数据：
，
，
，
）
已知：抛物线
经过B（3，0）、C（0，3）两点，顶点为A．
求：（1）抛物线的表达式；
（2）顶点A的坐标．
在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式
+（b-3）2=0，（c-4）2≤0.
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（m，
），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．