如图, 为 的直径, 为 上一点, 为 延长线上一点, .
(1)求证: 为 的切线;
(2)线段 分别交 , 于点 , 且 , 的半径为5, ,求 的长.

某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元.
(1)第二周单价降低x元后,这周销售的销量为(用x的关系式表示).
(2)求这批旅游纪念品第二周的销售价格.
在下图中,每个正方形由边长为1 的小正方形组成:
| 正方形边长 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
| 黑色小正方形个数 |
1 |
4 |
5 |
8 |
(1)观察图形,请填写下列表格;
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1,白色小正方形的个数
为P2,问是否存在偶数n,使P2="5" P1?若存在,请求出n的值;若不存在,请说明理由.
定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
已知:如图, AB是⊙O的直径,点C、D为圆上两点,且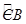 =
=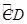 ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.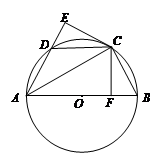
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=8,求△ACD的面积.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.