如图,在 中, , ,点 为 的中点, ,将 绕点 顺时针旋转 度 ,角的两边分别交直线 于 、 两点,设 、 两点间的距离为 , , 两点间的距离为 .
小涛根据学习函数的经验,对函数 随自变量 的变化而变化的规律进行了探究.
下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是 , 两点间的距离 进行取点、画图、测量,分别得到了 与 的几组对应值:
|
0 |
0.30 |
0.50 |
1.00 |
1.50 |
2.00 |
2.50 |
|
3.00 |
3.50 |
3.68 |
3.81 |
3.90 |
3.93 |
4.10 |
|
|
2.88 |
2.81 |
2.69 |
2.67 |
2.80 |
3.15 |
|
3.85 |
5.24 |
6.01 |
6.71 |
7.27 |
7.44 |
8.87 |
请你通过计算,补全表格;
(2)描点、连线,在平面直角坐标系 中,描出表格中各组数值所对应的点 ,并画出函数 关于 的图象.

(3)探究性质:随着自变量 的不断增大,函数 的变化趋势: .
(4)解决问题:当 时, 的长度大约是 .(保留两位小数).

已知:Rt△A′BC′和 Rt△ABC重合,∠A′C′B=∠ACB=90°,∠BA′C′=∠BAC=30°,现将Rt△A′BC′ 绕点B按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C′C和线段AA′相交于点D,连接BD.
(1)当α=60°时,A’B 过点C,如图1所示,判断BD和A′A之间的位置关系,不必证明;
(2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;
(3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.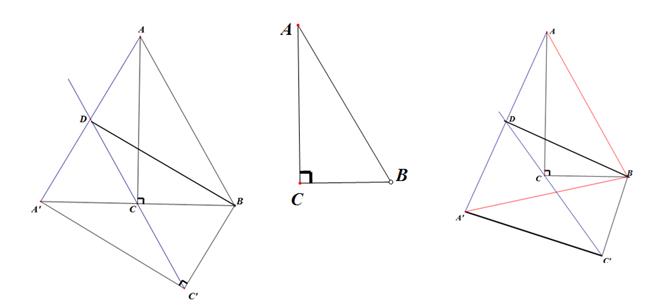
在平面直角坐标系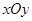 中,抛物线
中,抛物线 过点
过点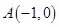 ,
,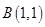 ,与
,与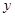 轴交于点
轴交于点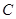 .
.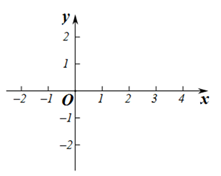
(1)求抛物线 的函数表达式;
的函数表达式;
(2)若点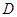 在抛物线
在抛物线 的对称轴上,当
的对称轴上,当 的周长最小时,求点
的周长最小时,求点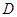 的坐标;
的坐标;
(3)在抛物线 的对称轴上是否存在点
的对称轴上是否存在点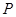 ,使
,使 成为以
成为以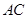 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点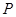 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
在四边形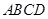 中,对角线
中,对角线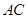 与
与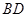 交于点
交于点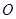 ,
,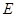 是
是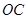 上任意一点,
上任意一点,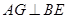 于点
于点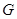 ,交
,交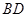 于点
于点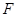 .
.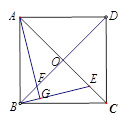

(1)如图1,若四边形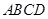 是正方形,判断
是正方形,判断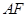 与
与 的数量关系;
的数量关系;
明明发现,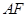 与
与 分别在
分别在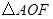 和
和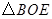 中,可以通过证明
中,可以通过证明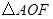 和
和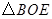 全等,得到
全等,得到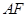 与
与 的数量关系;请回答:
的数量关系;请回答: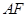 与
与 的数量关系是.
的数量关系是.
(2) 如图2,若四边形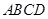 是菱形,
是菱形, 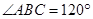 ,请参考明明思考问题的方法,求
,请参考明明思考问题的方法,求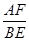 的值.
的值.
如图,在⊙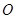 中,
中,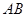 为直径,
为直径,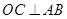 ,弦
,弦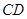 与
与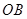 交于点
交于点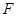 ,过点
,过点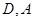 分别作⊙
分别作⊙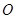 的切线交于点
的切线交于点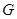 ,且GD与
,且GD与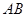 的延长线交于点
的延长线交于点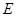 .
.
(1)求证: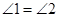 ;
;
(2)已知: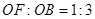 ,⊙
,⊙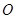 的半径为
的半径为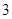 ,求
,求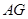 的长.
的长.
为弘扬中华传统文化,某学校决定开设民族器乐选修课.为了更贴合学生的兴趣,对学生最喜爱的一种民族乐器进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题: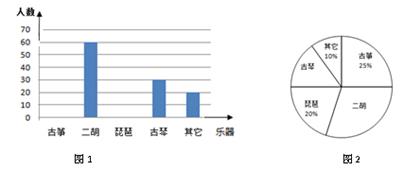
(1)在这次抽样调查中,共调查名学生;
(2)请把条形图(图1)补充完整;
(3)求扇形统计图(图2)中,二胡部分所对应的圆心角的度数;
(4)如果该校共有学生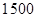 名,请你估计最喜爱古琴的学生人数.
名,请你估计最喜爱古琴的学生人数.