通过对下面数学模型的研究学习,解决问题.
【模型呈现】
如图,在 , ,将斜边 绕点 顺时针旋转 得到 ,过点 作 于点 ,可以推理得到 ,进而得到 , .
我们把这个数学模型称为“ 型”.
推理过程如下:

【模型应用】
如图,在 内接于 , , ,将斜边 绕点 顺时针旋转一定的角度得到 ,过点 作 于点 , , ,连接 交 于点 .
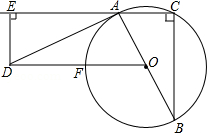
(1)求证: 是 的切线;
(2)连接 交 于点 ,连接 .求证: .
随机抽取某理发店一周的营业额如下表(单位:元)
|
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
合计 |
|
540 |
680 |
760 |
640 |
960 |
2200 |
1780 |
7560 |
(1)求该店本周的日平均营业额;
(2)如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额,你认为是否合理?如果合理,请说明理由;如果不合理,请设计一个方案,并估计该店当月(按30天计算)的营业总额.
如图,在四边形 中, , . 是四边形 内一点,且 .求证:
(1) ;
(2)四边形 是菱形.

刘阿姨到超市购买大米,第一次按原价购买,用了105元,几天后,遇上这种大米8折出售,她用140元又买了一些,两次一共购买了 .这种大米的原价是多少?
如图,在数轴上,点 、 分别表示数1、 .
(1)求 的取值范围;
(2)数轴上表示数 的点应落在 .
.点 的左边 .线段 上 .点 的右边

在数学兴趣小组活动中,小亮进行数学探究活动. 是边长为2的等边三角形, 是 上一点,小亮以 为边向 的右侧作等边三角形 ,连接 .

(1)如图1,当点 在线段 上时, 、 相交于点 ,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点 在线段 上运动时,点 也随着运动,若四边形 的面积为 ,求 的长.
(3)如图2,当点 在 的延长线上运动时, 、 相交于点 ,请你探求 的面积 与 的面积 之间的数量关系.并说明理由.
(4)如图2,当 的面积 时,求 的长.