随机抽取某理发店一周的营业额如下表（单位：元）
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
合计 |
540 |
680 |
760 |
640 |
960 |
2200 |
1780 |
7560 |
（1）求该店本周的日平均营业额；
（2）如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额，你认为是否合理？如果合理，请说明理由；如果不合理，请设计一个方案，并估计该店当月（按30天计算）的营业总额．
为了增强公民的节水意识，合理利用水资源，某市规定用水收费标准：每户每月的用水量不超过6吨时，水费按每吨m元收费，超过6吨时，不超过部分仍按每吨m元收费，超出部分按每吨n元收费。该市某户今年9、10月份的用水量和所交水费如下表所示，设某户每月用水量x吨，应交水费y元。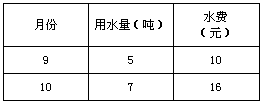
（1）求m、n的值；
（2）分别写出用水不超过6吨和超过6吨时，y关于x的函数关系式；
（3）若该户11月份用水10吨，求11月份应交水费。
以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连结BE、CF，
（1）试探索BE和CF长度的关系？并证明；
（2）你能找到哪两个图形可以通过旋转而互相得到，并指出旋转中心和旋转角。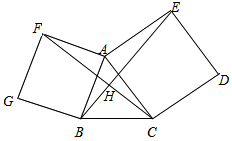
小文家与学校相距1000米。某天小文上学时忘了带一本书，走了一段时间才想起，于是返回家拿书，然后加快速度赶到学校。下图是小文与家的距离y(米)关于时间x(分钟)的函数图象。请你根据图象中给出的信息，解答下列问题：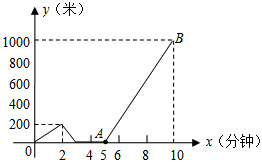
（1）小文走了多远才返回家拿书？
（2）求线段AB所在直线的函数解析式；
（3）当
分钟时，求小文与家的距离。
△ABC在平面直角坐标系中的位置如图所示。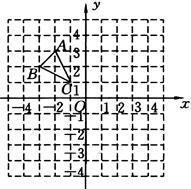
（1）作出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标；
（2）作出将△ABC绕点O顺时针旋转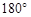
后的△A2B2C2。
作出函数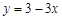
的图象，并根据图象回答下列问题：
（1）y的值随x的增大而；
（2）图象与x轴的交点坐标是；与y轴的交点坐标是；
（3）当x时，y≥0；
（4）函数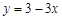的图象与坐标轴所围成的三角形的面积是________________。