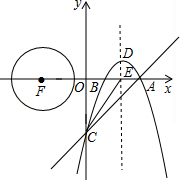
如图,直线 交 轴于点 ,交 轴于点 ,点 的坐标为 ,抛物线 经过 , , 三点,抛物线的顶点为点 ,对称轴与 轴的交点为点 ,点 关于原点的对称点为 ,连接 ,以点 为圆心, 的长为半径作圆,点 为直线 上的一个动点.
(1)求抛物线的解析式;
(2)求 周长的最小值;
(3)若动点 与点 不重合,点 为 上的任意一点,当 的最大值等于 时,过 , 两点的直线与抛物线交于 , 两点(点 在点 的左侧),求四边形 的面积.
一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1
个单位.用实数加法表示为 3+(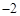 )=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移
)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移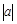 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移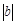 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 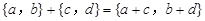 .
.
(1)计算:{3,1}+{1,2};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点O吗? 在图1中画出四边形OABC.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
李晖到“宇泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
| 营业员 |
小俐 |
小花 |
| 月销售件数(件) |
200 |
150 |
| 月总收入(元) |
1400 |
1250 |
假设月销售件数为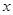 件,月总收入为
件,月总收入为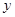 元,销售每件奖励
元,销售每件奖励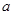 元,营业员月基本工资为
元,营业员月基本工资为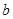 元.
元.
(1)求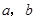 的值;
的值;
(2)若营业员小俐某月总收入不低于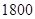 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件?
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为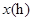 ,两车之间的距离为
,两车之间的距离为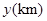 ,图中的折线表示
,图中的折线表示 与
与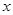 之间的函数关系.根据图象进行以下探究:
之间的函数关系.根据图象进行以下探究: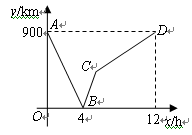
信息读取:
(1)甲、乙两地之间的距离为km;
(2)请解释图中点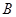 的实际意义;
的实际意义;
图象理解:
(3)求慢车和快车的速度;
(4)求线段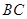 所表示的
所表示的 与
与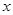 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量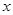 的取值范围;
的取值范围;
问题解决:
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
某加油站五月份营销一种油品的销售利润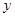 (万元)与销售量
(万元)与销售量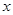 (万升)之间函数关系的图象如图中折线所示,该加油站截止到13日调价时的销售利润为4万元,截止至15日进油时的销售利润为5.5万元.(销售利润=(售价-成本价)×销售量)
(万升)之间函数关系的图象如图中折线所示,该加油站截止到13日调价时的销售利润为4万元,截止至15日进油时的销售利润为5.5万元.(销售利润=(售价-成本价)×销售量)
请你根据图象及加油站五月份该油品的所有销售记录提供的信息,解答下列问题: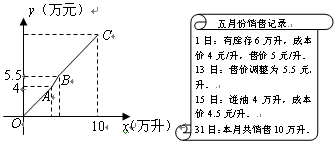
(1)求销售量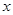 为多少时,销售利润为4万元;
为多少时,销售利润为4万元;
(2)分别求出线段AB与BC所对应的函数关系式;
(3)我们把销售每升油所获得的利润称为利润率,那么,在OA、AB、BC三段所表示的销售信息中,哪一段的利润率最大?(直接写出答案)
(1)观察与发现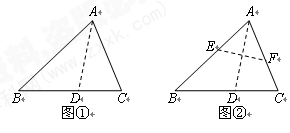
小明将三角形纸片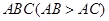 沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到
沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到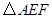 (如图②).小明认为
(如图②).小明认为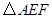 是等腰三角形,你同意吗?请说明理由.
是等腰三角形,你同意吗?请说明理由.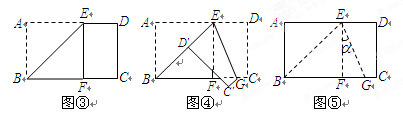
(2)实践与运用
将矩形纸片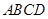 沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点
沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点 处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中
处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中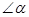 的大小.
的大小.