如图,抛物线 与 轴交于 、 两点, 是 轴上一点,连接 ,延长 交抛物线于点 .
(1)求此抛物线的解析式;
(2)若 点在第一象限,过点 作 轴于点 , 与 的面积比为 ,求出点 的坐标;
(3)若 是 轴上的动点,过 点作与 轴平行的直线交抛物线于 、 两点,是否存在点 ,使 ?若存在,请求出点 的坐标;若不存在,请说明理由.

泰州新星电子科技公司积极应对世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线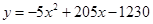 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?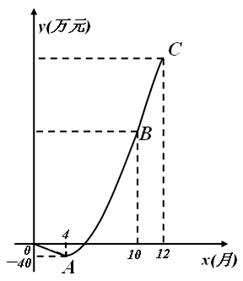
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC.AD.BC之间的数量关系,并说明理由;
(3)若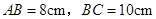 ,求大圆与小圆围成的圆环的面积.(结果保留π)
,求大圆与小圆围成的圆环的面积.(结果保留π)
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转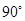 ,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.
,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.
星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15 .如图所示,已知AB与地面的夹角为 60
.如图所示,已知AB与地面的夹角为 60 ,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据
,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据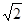 ≈1.4
≈1.4 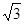 ≈1.7)
≈1.7)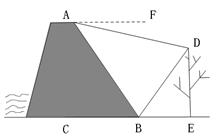
一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4,小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.