如图,四边形 是边长为4的正方形,点 为 边上任意一点(与点 、 不重合),连接 ,过点 作 交 于点 ,且 ,过点 作 ,交 于点 ,连接 、 ,设 .
(1)求点 的坐标(用含 的代数式表示);
(2)试判断线段 的长度是否随点 的位置的变化而改变?并说明理由.
(3)当 为何值时,四边形 的面积最小;
(4)在 轴正半轴上存在点 ,使得 是等腰三角形,请直接写出不少于4个符合条件的点 的坐标(用含 的式子表示).

如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.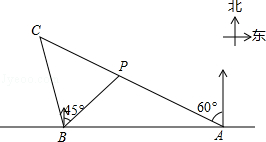
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)
如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=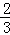 .
.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
为从小明和小刚中选出一人去观看元旦文艺汇演,现设计了如下游戏,规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏是否公平.
今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.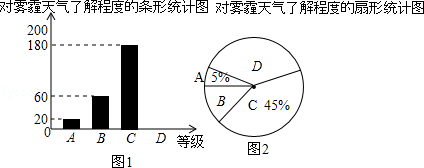
对雾霾了解程度的统计表:
| 对雾霾的了解程度 |
百分比 |
| A.非常了解 |
5% |
| B.比较了解 |
m |
| C.基本了解 |
45% |
| D.不了解 |
n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是多少度;
(3)请补全条形统计图.
已知关于x的一元二次方程(a﹣3)x2﹣4x﹣1=0
(1)若方程有两个相等的实数根,求a的值及此时方程的根;
(2)若方程有两个不相等的实数根,求a的取值范围.