2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量 (个 与售价 (元 之间的函数关系 ;
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?
(南充)某学校要了解学生上学交通情况,选取九年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知九年级乘公交车上学的人数为50人.
(1)九年级学业生中,骑自行车和乘公交车上学哪个更多?多多少人?
(2)如果全校有学生2000人,学校准备的400个自行车停车位是否足够?
(成都)(本小题满人8分)国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步晋及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)求获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用树状图或列表的方法求恰好达到A,B两所学校的概率.
(乐山)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
(乐山)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=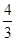 .
.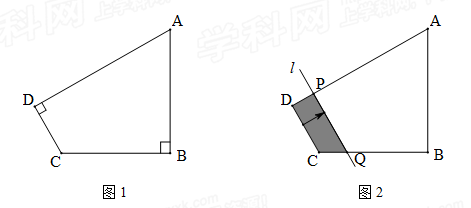
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为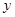 ,求
,求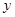 与
与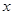 的函数关系式,并求出自变量
的函数关系式,并求出自变量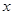 的取值范围.
的取值范围.
(乐山)如图,正比例函数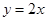 的图象与反比例函数
的图象与反比例函数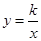 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.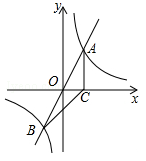
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.