如图，⊙M的圆心M(−1,2)，⊙M经过坐标原点O，与y轴交-优题课

题文

如图， $⊙ M$ 的圆心 $M (- 1, 2)$ ， $⊙ M$ 经过坐标原点 $O$ ，与 $y$ 轴交于点 $A$ ．经过点 $A$ 的一条直线 $l$ 解析式为： $y = - \frac{1}{2} x + 4$ 与 $x$ 轴交于点 $B$ ，以 $M$ 为顶点的抛物线经过 $x$ 轴上点 $D (2, 0)$ 和点 $C (- 4, 0)$ ．

（1）求抛物线的解析式；

（2）求证：直线 $l$ 是 $⊙ M$ 的切线；

（3）点 $P$ 为抛物线上一动点，且 $PE$ 与直线 $l$ 垂直，垂足为 $E$ ； $PF / / y$ 轴，交直线 $l$ 于点 $F$ ，是否存在这样的点 $P$ ，使 $ΔPEF$ 的面积最小．若存在，请求出此时点 $P$ 的坐标及 $ΔPEF$ 面积的最小值；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数的性质待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

在平面直角坐标系中，已知抛物线(b，c为常数)的顶点为P，等腰直角三角形ABC的顶点A的坐标为(0，–1)，C的坐标为(4，3)，直角顶点B在第四象限．
(1)如图，若该抛物线过A，B两点，求b，c的值；
(2)平移(1)中的抛物线，使顶点P在直线AC上滑动，且与直线AC交于另一点Q．
①点M在直线AC下方，且为平移前(1)中的抛物线上的点，当以M，P，Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时，求点M的坐标；
②取BC的中点N，连接NP，BQ．当取最大值时，点Q的坐标为________.

（1）如图1，点E、F分别是正方形ABCD的边BC、CD上的点，∠EAF=45°，连接EF，
则EF、BE、FD之间的数量关系是：EF=BE+FD．连结BD，交AE、AF于点M、N，且MN、BM、DN满足，请证明这个等量关系；
（2）在△ABC中， AB=AC，点D、E分别为BC边上的两点．
①如图2，当∠BAC=60°，∠DAE=30°时，BD、DE、EC应满足的等量关系是__________________；
②如图3，当∠BAC=，(0°<<90°)，∠DAE=时，BD、DE、EC应满足的等量关系是____________________．【参考：】

如图，在平面直角坐标系中，直线与抛物线y＝ax²＋bx－3（a≠0）交于A、B两点，点A在x轴上，点B的纵坐标为5．点P是直线AB下方的抛物线上的一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．
（1）求抛物线的解析式；
（2）设点P的横坐标为m．
①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；
②连结PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积比为1:2．若存在，直接写出m的值；若不存在，请说明理由．

如图1，在△ABC中，E、D分别为AB、AC上的点，且ED//BC，O为DC中点，连结EO并延长交BC的延长线于点F，则有S_{四边形EBCD}=S_△_EBF.
（1）如图2，在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．将直线MN绕着点P旋转的过程中发现，当直线MN满足某个条件时，△MON的面积存在最小值．直接写出这个条件:_______________________.
（2）如图3，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3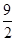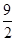）、（，）、（4、2），过点P的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．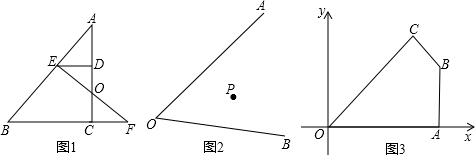

由平谷统计局2013年12月发布的数据可知，我区的旅游业蓬勃发展，以下是根据近几年我区旅游业相关数据绘制统计图的一部分：

请你根据以上信息解答下列问题：
（1）计算2012年平谷区旅游区点营业收入占全区旅游营业收入的百分比，并补全扇形统计图；
（2）2012年旅游区点的收入为2.1万元，请你计算2012年平谷区旅游营业收入，并补全条形统计图 (结果保留一位小数)；
（3）如果今年我区的旅游营业收入继续保持2013年的增长趋势，请你预测我区今年的旅游营业收入 (结果保留一位小数) .

试卷网试题网古诗词网作文网范文网