（1）如图1，点E、F分别是正方形ABCD的边BC、CD上的点，∠EAF=45°，连接EF，
则EF、BE、FD之间的数量关系是：EF=BE+FD．连结BD，交AE、AF于点M、N，且MN、BM、DN满足
，请证明这个等量关系；
（2）在△ABC中， AB=AC，点D、E分别为BC边上的两点．
①如图2，当∠BAC=60°，∠DAE=30°时，BD、DE、EC应满足的等量关系是__________________；
②如图3，当∠BAC=
，(0°<<90°)，∠DAE=
时，BD、DE、EC应满足的等量关系是____________________．【参考：
】
如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．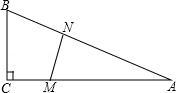
（1）当t为何值时，∠AMN=∠ANM？
（2）当t为何值时，△AMN的面积最大？并求出这个最大值．
如图，已知AD为⊙O的直径，B为AD延长线上一点，BC与⊙O切于C点，∠A=30°．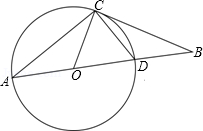
求证：（1）BD=CD；（2）△AOC≌△CDB．
学校开展综合实践活动中，某班进行了小制作评比，作品上交时间为5月11日至5月30日，评委们把同学们上交作品的件数按5天一组分组统计，绘制了频数分布直方图如下，小长方形的高之比为：2：5：2：1．现已知第二组的上交作品件数是20件．求：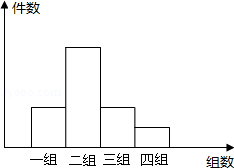
（1）此班这次上交作品共 件；
（2）评委们一致认为第四组的作品质量都比较高，现从中随机抽取2件作品参加学校评比，小明的两件作品都在第四组中，他的两件作品都被抽中的概率是多少？（请写出解答过程）
如图，在矩形ABCD中，AB=6，BC=8，沿直线MN对折，使A、C重合，直线MN交AC于O．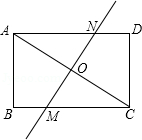
（1）求证：△COM∽△CBA；
（2）求线段OM的长度．
在学校组织的游艺晚会上，掷飞标游艺区游戏规则如下：如图掷到A区和B区的得分不同，A区为小圆内部分，B区为大圆内小圆外的部分（掷中一次记一个点）．现统计小华、小芳和小明掷中与得分情况如下：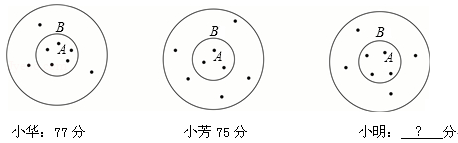
（1）求掷中A区、B区一次各得多少分？
（2）依此方法计算小明的得分为多少分？