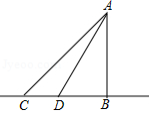
如图,有一铁塔 ,为了测量其高度,在水平面选取 , 两点,在点 处测得 的仰角为 ,距点 的10米 处测得 的仰角为 ,且 、 、 在同一水平直线上,求铁塔 的高度(结果精确到0.1米,
一个四边形的周长是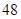 cm,已知第一条边的长是
cm,已知第一条边的长是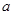 cm,第二条边长比第一条边长的
cm,第二条边长比第一条边长的 倍还少
倍还少 cm,第三条边长等于第一、第二条边长的和。请通过计算用含
cm,第三条边长等于第一、第二条边长的和。请通过计算用含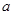 的代数式表示第四条边的长.
的代数式表示第四条边的长.
求 的值,其中
的值,其中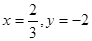 .
.
某书店举行图书促销会,每位促销人员以销售50本为基准,超过记为正,不足的记为负,其中10名促销人员的销售结果如下(单位:本):
4,2,3,-7,-3,-8,3,4,8,-1.
(1)这组促销人员的总销售量超过还是不足总销售基准?相差多少?
(2)如销售图书每本的利润为2.7元,此次促销会所得总利润为多少元?(结果保留整数)
化简:
(1) (2)
(2)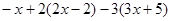
某家电生产企业根据市场调查分析,决定调整新产品方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且空调至少生产60台.设生产彩电x台,生产冰箱y台.已知生产这些家电新产品每台所需工时和每台产值如下表:
| 家电名称 |
彩电 |
冰箱 |
空调 |
| 工时 |
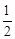 |
 |
 |
| 产值(千元) |
4 |
3 |
2 |
(1)用含x,y的式子表示生产空调的台数;
(2)求出y与x之间的函数关系式;
(3)每周应生产彩电、冰箱、空调各多少台,才能使产值最高,最高产值是多少千元?