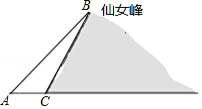
数学“综合与实践”课中，老师带领同学们来到娄底市郊区，测算如图所示的仙女峰的高度，李红盛同学利用已学的数学知识设计了一个实践方案，并实施了如下操作：先在水平地面 处测得山顶 的仰角 为 ，再由 沿水平方向前进377米到达山脚 处，测得山坡 的坡度为 ，请你求出仙女峰的高度（参考数据：
如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB=6cm，AD=2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/ 秒的速度向终点B移动，点Q以1厘米/ 秒的速度向D移动，当有一点到达终点时，另一点也停止运动。设运动的时间为t ，问：
（1）当t=1秒时，四边形BCQP面积是多少？
（2）当t为何值时，点P和点Q距离是3cm？
（3）当t=时， 以点P、Q、D为顶点的三角形是等腰三角形.（直接写出答案）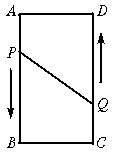
端午节期间，某食品店平均每天可卖出300只粽子，卖出1只粽子的利润是1元.经调查发现，零售单价每降0.1元，每天可多卖出100只粽子.为了使每天获取的利润更多，该店决定把零售单价下降m（0﹤m﹤1）元.
（1）零售单价下降m元后，该店平均每天可卖出只粽子，利润为元（用含m的代数式表示）；
（2）在不考虑其他因素的条件下，当m定为多少时，才能使该店每天获取的利润是420元并且卖出的粽子更多？
已知：如图：架在消防车上的云梯AB的坡比为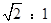
，云梯AB的长为
m，云梯底部离地面1.5m（即BC=1.5m）.求云梯顶端离地面的距离AE.
解方程
（1）
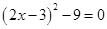（2）
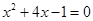
如图，在△ABC中，∠B=90°，AB=BC=10cm，点P从A出发沿射线AB 以1cm/s的速度作直线运动，点Q从C出发沿边BC的延长线以2cm/s的速度作直线运动．如果P，Q分别从A，B同时出发，经过几秒，△PCQ的面积为24cm2 ?