列方程组解应用题:
某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如表:
批发价(元 |
零售价(元 |
|
黑色文化衫 |
10 |
25 |
白色文化衫 |
8 |
20 |
假设文化衫全部售出,共获利1860元,求黑白两种文化衫各多少件?
如图,在△ABC中,AB=AC,D为BC边上一点,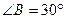 ,
,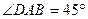 .
.求
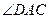 的度数;
的度数;求证:AB=CD.

如图,已知AC⊥BD于点E,且点E是线段BD的中点,AB=CD.
求证:△ABE≌△CDE. 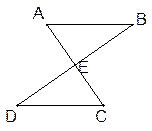
如图,△ABC的顶点都在平面直角坐标系的网格点上。画出与△ABC关于x轴对称的图形,并记为△A1B1C1;
写出点A1、B1、C1的坐标,求△A1B1C1的面积;
已知△ABC的内部有一点P(a,b),则点P在△A1B1C1的对应点P1的坐标是__________.

解方程

计算:

如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”。如4=22-02,12=42-22,20=62-42,因此,4,12,20这三个数都是神秘数。28和2012这两个数是神秘数吗?为什么?
设两个连续偶数为2k+2和2k(其中k取非负数),由这两个连续偶数构成的神秘数是4的倍数吗?为什么?
两个连续奇数的平方差(取正数)是神秘吗?为什么?