阅读理解题:
定义:如果一个数的平方等于 ,记为 ,这个数 叫做虚数单位,把形如 , 为实数)的数叫做复数,其中 叫这个复数的实部, 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: ;
;
根据以上信息,完成下列问题:
(1)填空: , ;
(2)计算: ;
(3)计算: .
某中学在校内安放了几个圆柱形饮水桶的木制支架(如图①),若不计木条的厚度,其俯视图如图②所示,已知AD垂直平分BC,AD=BC=40cm,则圆柱形饮水桶的底面半径的最大值是____▲ _____cm.
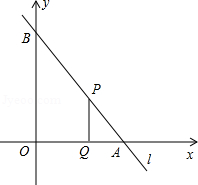
如图,直线l与x轴、y轴的正半轴分别交于A、B两点,OA、OB的长分别是关于x的方程x2﹣14x+4(AB+2)=0的两个根(OB>OA),P是直线l上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q求tan∠BAO的值
若S△PAQ=
 S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;
S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;当点P在线段AB上运动时,在y轴上是否存在点M,使△MPQ为等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
如图,矩形OABC的面积为15,其OA边在x轴上,OC边在y轴上,且OA比OC大2,函数y= (k≠0)的图象经过点B.
(k≠0)的图象经过点B.求k的值.
将矩形OABC分别沿AB,BC翻折,得到矩形MABD和矩形NCBE.线段MD、NE分别与函数y=
 (k≠0)的图象交于F、G两点,求线段FG所在直线的解
(k≠0)的图象交于F、G两点,求线段FG所在直线的解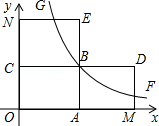
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲、乙两厂的印刷费用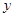 (千元)与证书数量
(千元)与证书数量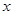 (千个)的函数关系图象分别如图中甲、乙所示.
(千个)的函数关系图象分别如图中甲、乙所示.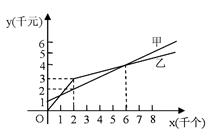
请你直接写出甲厂的制版费及
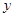 甲与
甲与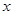 的函数解析式,并求出其证书印刷单价
的函数解析式,并求出其证书印刷单价当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
如果甲厂想把8千个证书的印制工作承揽下来,在不降低制版费的前提下,每
个证书最少降低多少元?
如图,△ABC内接于⊙O, CA=CB,CD∥AB且与OA的延长线交于点D.
判断CD与⊙O的位置关系并说明理由;
若∠ACB=120°,OA=2,求CD的长;